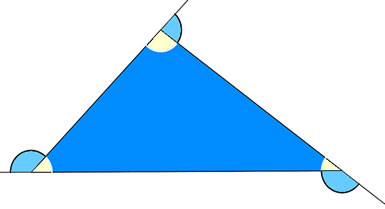
Os polígonos são figuras geométricas planas fechadas formadas por segmentos de reta que possuem apenas suas extremidades como ponto comum. São compostos por vértices, lados, ângulos internos e externos, e diagonais. Dependendo de suas características, podem ser classificados em convexos ou côncavos. Se as medidas de seus lados e ângulos forem todas iguais, são chamados de polígonos regulares.
Recebem nomes especiais dependendo da quantidade de lados que possuem. É possível calcular o perímetro e a área dos polígonos, e no caso de polígonos convexos existe uma maneira de calcular também a soma de seus ângulos internos e externos.
Leia também: Afinal, o que são ângulos?
Tópicos deste artigo
- 1 - Resumo sobre polígonos
- 2 - Videoaula sobre polígonos
- 3 - O que são polígonos?
- 4 - Elementos dos polígonos
- 5 - Qual a classificação dos polígonos?
- 6 - Qual a nomenclatura dos polígonos?
- 7 - Perímetro dos polígonos
- 8 - Área dos polígonos
- 9 - Soma dos ângulos internos de um polígono
- 10 - Soma dos ângulos externos de um polígono
- 11 - Exercícios resolvidos sobre polígonos
Resumo sobre polígonos
-
Polígonos são figuras planas fechadas, formadas por segmentos de reta.
-
Seus elementos são: vértices, lados, ângulos (internos e externos) e diagonais.
-
Podem ser classificados em convexos ou côncavos.
-
Podem ser classificados em regulares ou irregulares.
-
Triângulos e quadriláteros são polígonos com três e quatro lados, respectivamente.
-
Polígonos com cinco ou mais lados recebem seus nomes de acordo com seu número de lados.
-
O perímetro é a soma dos lados do polígono, e a área é a medida de toda a sua superfície.
-
A fórmula da soma dos ângulos internos de um polígono convexo de n lados é: \(S_n=(n-2)⋅180°\).
-
A soma dos ângulos externos de um polígono convexo é sempre 360°.
Videoaula sobre polígonos
O que são polígonos?
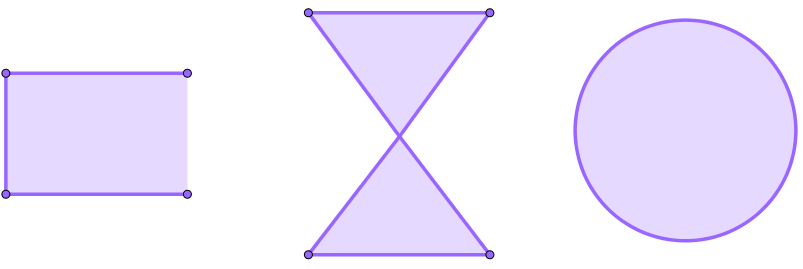
Polígonos são figuras planas fechadas formadas por segmentos de reta conectados por suas extremidades. A palavra polígono deriva da junção de duas palavras de origem grega: póly (vários) e gonía (ângulos).
Vamos considerar que, para uma figura ser classificada como um polígono, apenas as extremidades dos segmentos de reta que a formam se interligam. Portanto, figuras que não são fechadas, figuras que são compostas por segmentos que se cruzam e figuras que apresentam linhas curvas não serão denominadas polígonos.
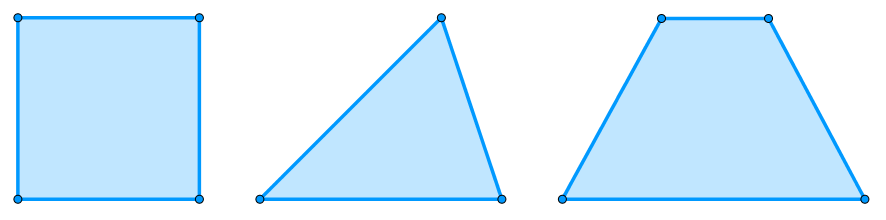
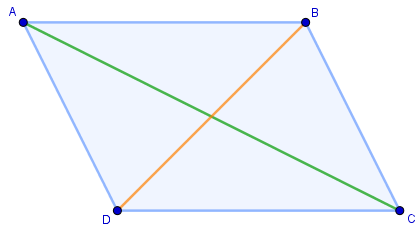
Elementos dos polígonos
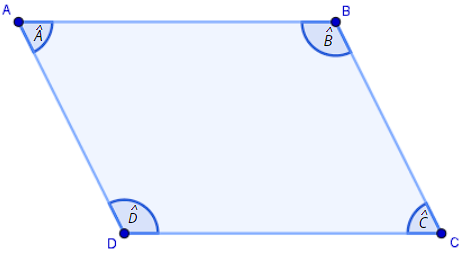
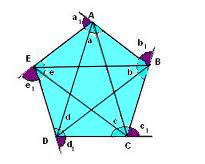
Como polígonos são figuras planas fechadas por segmentos de reta, podemos destacar entre seus principais elementos: os vértices, lados, ângulos internos, diagonais e ângulos externos.
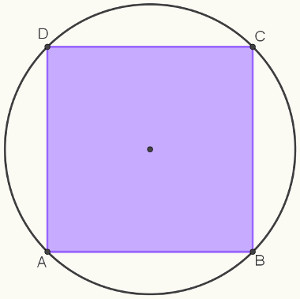
Na figura acima, temos as seguintes representações:
-
Vértices: cada um dos pontos A, B, C e D.
-
Lados: os segmentos de reta \(\overline{AB}\), \(\overline{BC}\), \(\overline{CD}\) e \(\overline{DA}\).
-
Ângulos internos: as aberturas \(\hat{A}\), \(\hat{B}\), \(\hat{C}\) e \(\hat{D}\) internas formadas pela união de dois lados adjacentes do polígono.
-
Diagonais: são os segmentos de reta cujas extremidades são dois vértices não adjacentes do polígono.
-
Ângulos externos: são os ângulos suplementares adjacentes aos ângulos internos do polígono.
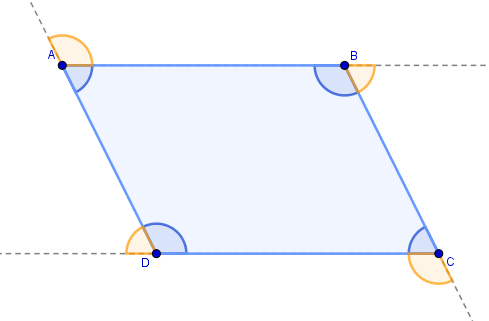
Na figura acima é possível observar que cada ângulo externo é suplementar ao seu correspondente ângulo interno, ou seja, a soma deles resulta em um ângulo de 180°.
Observação: Um polígono possui o mesmo número de vértices, lados e ângulos (internos e externos). Por exemplo, um triângulo possui três vértices, três lados e três ângulos (internos e externos).
Saiba mais: Propriedades dos ângulos alternos internos e externos
Qual a classificação dos polígonos?
É possível classificar um polígono de acordo com suas características ou dependendo da medida de seus lados e ângulos. Veja a seguir as classificações mais usuais.
-
Polígono convexo e côncavo
Um polígono pode ser classificado como convexo ou não convexo (também chamado de côncavo).
Para ser convexo é necessário que quaisquer dois pontos do polígono possam ser ligados por um segmento de reta que esteja inteiramente contido nesse polígono. Se isso não for possível, esse polígono não é convexo e, portanto, é um polígono côncavo.
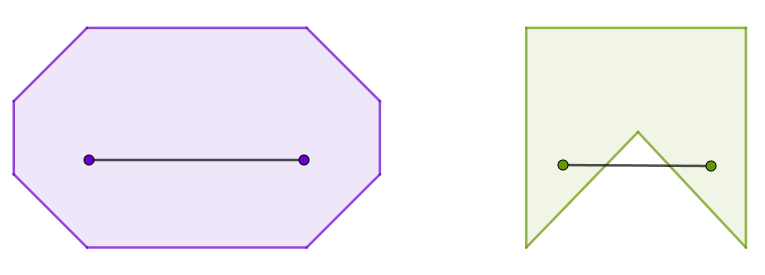
-
Polígono equiângulo
Um polígono é classificado como equiângulo se a medida de cada um de seus ângulos internos for a mesma dos demais ângulos internos.
Por exemplo, um quadrado é um polígono equiângulo, pois todos os seus ângulos internos medem 90°. Um triângulo equilátero também é um polígono equiângulo, pois cada um de seus ângulos internos mede 60°.
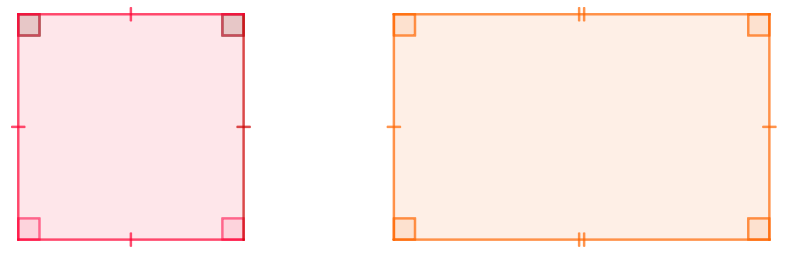
-
Polígonos regulares e irregulares
Um polígono convexo é dito regular se as medidas de seus lados e ângulos internos forem congruentes às medidas dos demais lados e ângulos internos.
Assim, basta que um lado ou ângulo não tenha a mesma medida dos demais para que um polígono não seja regular, sendo considerado, portanto, um polígono irregular.
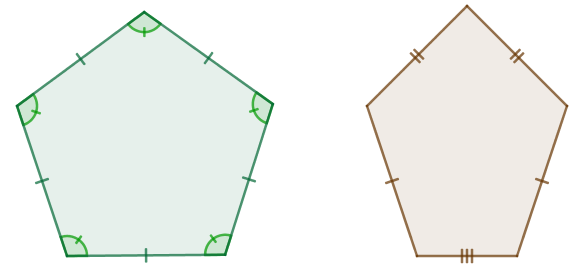
Observação: Perceba que um polígono regular é um polígono equiângulo, mas um polígono equiângulo pode não ser regular. Um exemplo disso é o retângulo, pois ele possui todos os ângulos internos com mesma medida (de 90°), mas seus lados podem ter medidas distintas.
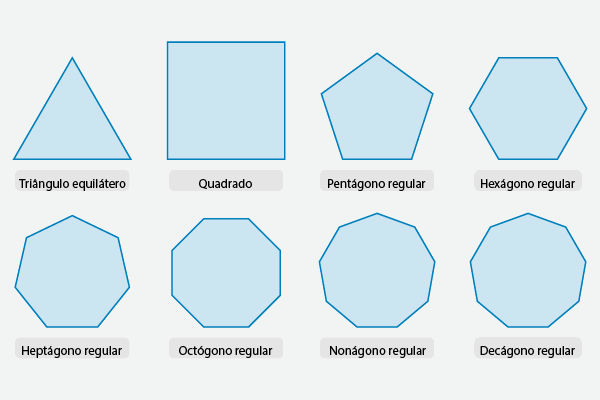
Qual a nomenclatura dos polígonos?
Polígonos com três lados são nomeados triângulos, e polígonos com quatro lados são nomeados quadriláteros. Estes, por sua vez, possuem algumas características que os diferem e, portanto, possuem muitas nomenclaturas distintas entre si (quadrados, retângulos, losangos, trapézios, paralelogramos, entre outras).
Porém, como visto anteriormente, a palavra polígono é referente a uma figura com muitos ângulos, e, por conta disso, os polígonos recebem nomes de acordo com o número de ângulos que possuem.
Para compor essa nomenclatura é utilizado um prefixo referente ao número de ângulos (ou lados) que ele possui, e completa-se esse nome com o sufixo “gono”.
Por exemplo:
Polígono com 5 lados: penta + gono = pentágono
Polígono com 6 lados: hexa + gono = hexágono
Polígono com 7 lados: hepta + gono = heptágono

Perímetro dos polígonos
O perímetro de um polígono corresponde à soma da medida de todos os seus lados. Portanto, para calcular essa soma é necessário conhecer a medida de todos os lados do polígono ou haver maneiras de obter essas medidas.
-
Exemplo: Calcule o perímetro de um retângulo cujo comprimento mede 5 cm e a largura mede 3 cm.
Um retângulo é um polígono de 4 lados cujos lados opostos possuem a mesma medida. Logo, se um lado mede 5 cm, o lado oposto a ele terá essa mesma medida, assim como ocorre com o lado oposto àquele com medida de 3 cm.
Portanto, o perímetro de um retângulo é dado por:
Perímetro do retângulo = 5 + 5 + 3 + 3 = 16 cm
Área dos polígonos
A área de um polígono é a medida da superfície que ele ocupa. Geralmente, é necessário saber algumas medidas específicas para encontrar sua área, como base e altura (no caso de triângulos e retângulos) ou a medida de diagonais (como ocorre com o losango), além das fórmulas gerais que dependem do polígono em questão.
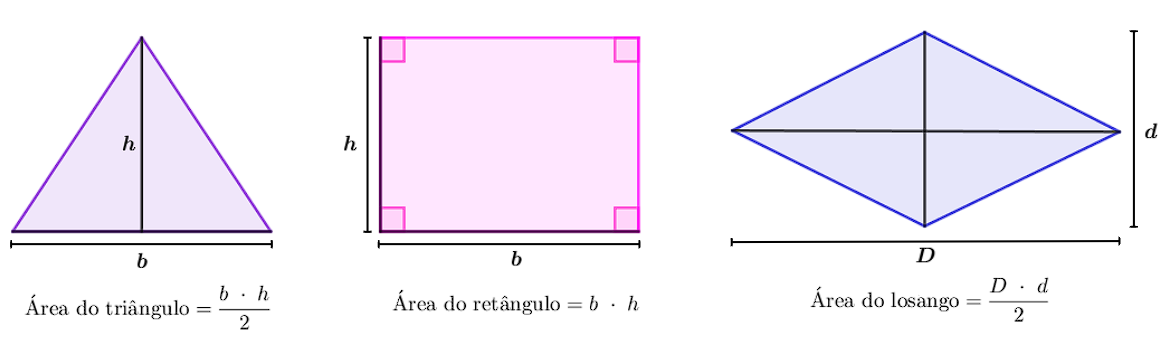
-
Exemplo 1: Calcule a área de um retângulo cuja base mede 5 cm e a altura mede 3 cm.
Sabe-se a medida da base do retângulo e sua altura. Assim, pode-se utilizar a fórmula da área do retângulo para calcular sua área:
Área do retângulo = \(b⋅h=(5\ cm) ⋅ (3\ cm)=15\ cm^2\)
-
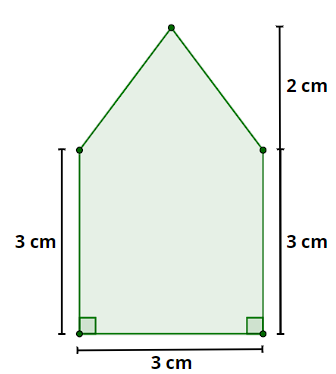
Exemplo 2: Calcule a área do polígono abaixo:
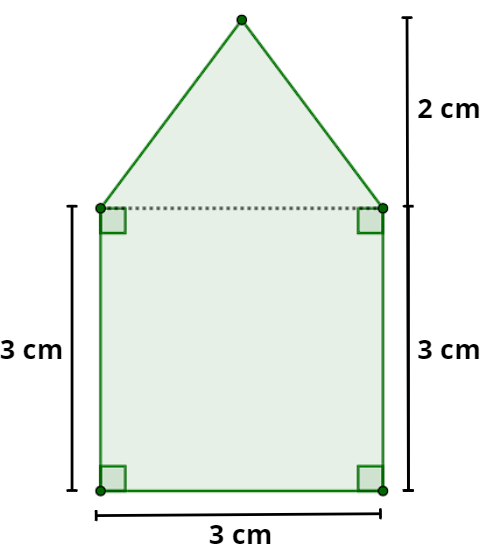
Perceba que esse polígono, mesmo não sendo comum, pode ser repartido em dois outros polígonos mais usuais:
Assim, para calcular a área do polígono original, basta calcular separadamente as áreas dos polígonos menores aos quais ele foi dividido: o quadrado e o triângulo.
Sabendo que o lado do quadrado mede 3 cm, sua área é dada por:
Área do quadrado = \(b⋅h=l⋅l=3⋅3=9\ cm^2\)
Já a base do triângulo mede 3 cm, enquanto sua altura mede 2 cm. Portanto, sua área é dada por:
Área do triângulo = \(\frac{b⋅h}2=\frac{3⋅2}2=3\ cm^2\)
Logo, a área do polígono original é de \(9+3=12\ cm^2\).
Leia também: Quais são as formas geométricas mais estudadas na Geometria?
Soma dos ângulos internos de um polígono
Existe uma fórmula que determina qual a soma dos ângulos internos de um polígono convexo.
Para encontrar essa soma, basta substituir o número de lados da figura, representado por n na fórmula abaixo:
Soma dos ângulos internos = \(S_n= (n-2)⋅180°\)
-
Exemplo: Qual a soma dos ângulos internos de um hexágono?
Um hexágono é um polígono com seis lados. Assim, substituindo n = 6 na fórmula, encontra-se a soma de seus ângulos internos:
\(S_n= (n-2)⋅180°\)
\(S_n= (6-2)⋅180°\)
\(S_n= 4⋅180°= 720°\)
Soma dos ângulos externos de um polígono
Independentemente de qual for o polígono convexo, a soma de seus ângulos externos será sempre igual a 360°.
Exercícios resolvidos sobre polígonos
Questão 1
(FAG 2016) Os ângulos internos de um quadrilátero medem 3x – 45 , 2x + 10 , 2x + 15 e x + 20 graus. O menor ângulo mede:
a) 90°
b) 65°
c) 45°
d) 105°
e) 80°
Resolução
Primeiramente, sabendo que um polígono é um quadrilátero (possui 4 lados), vejamos qual a soma de seus ângulos internos:
\(S_n= (4-2)⋅180°\)
\(S_n= 2⋅180°=360°\)
Agora, devemos somar seus ângulos internos e igualar a 360 , descobrindo assim o valor da incógnita x :
\((3x-45)+(2x+10)+(2x+15)+(x+20)=360\)
\((3x+2x+2x+x)+(-45+10+15+20)=360\)
\((8x)+(0)=360\)
\(x=\frac{360}8=45°\)
Por fim, basta substituir o valor de x = 45° em cada medida dos ângulos internos e observar qual deles é o menor:
\(3x-45=3⋅45-45=90°\)
\(2x+10=2⋅45+10=100°\)
\(2x+15=2⋅45+15=105°\)
\(x+20=45+20=65°\)
Portanto, o menor ângulo interno mede 65°.
A alternativa correta é a alternativa b.
Questão 2
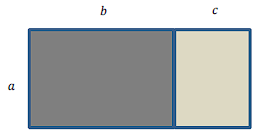
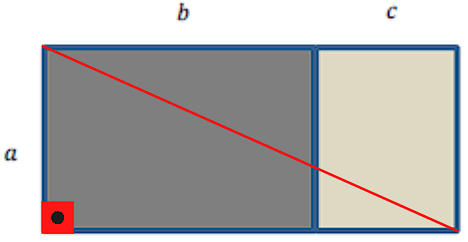
(Inep 2019) Dois retângulos são unidos para formar um retângulo maior, conforme a figura:
Quanto ao retângulo maior, qual a afirmativa correta?
a) Seu perímetro é dado pela expressão a + b + c;
b) Sua área pode ser dada pela expressão ab + c;
c) Sua diagonal é dada pela expressão \(\sqrt{a^2+b^2+c^2+2bc}\);
d) Sua área é dada por (a + b + c)2;
e) Sua diagonal pode ser dada pela expressão \(\sqrt{a^2+b^2+c^2}\).
Resolução
Perceba que as alternativas envolvem o perímetro, a área e a diagonal do novo retângulo. Calculemos então essas três informações e vejamos qual a alternativa correta.
O perímetro do retângulo é a soma de seus lados, ou seja,
\(P=a+a+(b+c)+(b+c)\)
\(P=2a+2(b+c)\)
A área é calculada através da fórmula da área de um retângulo de base (b+c) e altura a :
\(A=(b+c)⋅a\)
\(A=ab+ac\)
Por fim, a diagonal é o segmento que liga dois vértices não adjacentes, como é mostrado no esboço a seguir:
Agora perceba que a diagonal do retângulo corresponde à hipotenusa de um triângulo retângulo, cujos catetos medem a e (b + c). Portanto, a diagonal pode ser calculada por:
\(d^2=a^2+(b+c)^2\)
\(d^2=a^2+b^2+2 bc+c^2\)
\(d=\sqrt{a^2+b^2+c^2+2 bc}\)
Assim, a alternativa correta é a alternativa c.
Fontes
REZENDE, E.Q.F.; QUEIROZ, M. L. B. de. Geometria Euclidiana Plana: e construções geométricas. 2ª ed. Campinas: Unicamp, 2008.
SAMPAIO, Fausto Arnaud. Trilhas da matemática, 7º ano: ensino fundamental, anos finais. 1. ed. São Paulo: Saraiva, 2018.