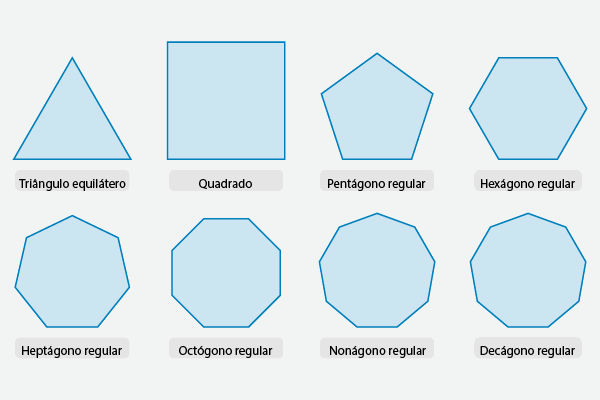
Os polígonos regulares são aqueles que têm todos os lados congruentes, ou seja, lados com a mesma medida. Alguns exemplos são o triângulo equilátero e o quadrado. Como eles têm lados com mesma medida, consequentemente, ao comparar-se os ângulos internos, eles também serão congruentes entre si.
Leia também: Como classificar os polígonos?
Tópicos deste artigo
- 1 - Resumo sobre polígonos regulares
- 2 - O que são polígonos regulares?
- 3 - Como calcular o perímetro dos polígonos regulares?
- 4 - Propriedades dos polígonos regulares
- 5 - Polígonos regulares x polígonos irregulares
- 6 - Exercícios resolvidos sobre polígonos regulares
Resumo sobre polígonos regulares
- Polígonos regulares são os que têm lados congruentes, ou seja, com a mesma medida.
- O polígono regular também tem ângulos internos congruentes entre si.
- Os ângulos externos de um polígono regular são congruentes e podem ser calculados quando dividimos 360º pelo número de lados.
- O valor de cada ângulo interno é a divisão entre a soma dos ângulos internos e o número de lados.
- O perímetro de um polígono regular é o comprimento do lado vezes o número de lados.
- O polígono irregular é o polígono que não tem todos os lados congruentes.
O que são polígonos regulares?
Os polígonos regulares são polígonos que têm lados com a mesma medida e ângulos com a mesma medida, ou seja, lados congruentes entre si e ângulos congruentes entre si. Temos o triângulo equilátero e o quadrado como principais exemplos; mas existem também pentágonos e hexágonos que são regulares.
Como calcular o perímetro dos polígonos regulares?
A medida do perímetro de um polígono regular pode ser calculada com a multiplicação do comprimento do lado pelo número de lados desse polígono, então podemos calcular o perímetro utilizando a fórmula:
\(P=n⋅l\)
l: medida do lado do polígono.
n: número de lados do polígono.
- Exemplo: Um hexágono regular tem lado medindo 9 cm, então quanto é o perímetro desse hexágono?
Resolução:
Sabemos que o hexágono é um polígono que tem 6 lados.
Como n = 6 e l = 9, temos que:
\(P = n⋅ l = 6⋅9=54cm\)
Veja também: O que são polígonos semelhantes?
Propriedades dos polígonos regulares
→ Ângulos dos polígonos regulares
Separando em dois casos, estudaremos os ângulos internos e os ângulos externos de um polígono regular, começando pelo ângulo interno. Sabemos que a fórmula para a soma dos ângulos internos é dada por:
\(S_i=180⋅(n-2)\)
Si : soma dos ângulos internos.
n: número de lados.
Para encontrar a medida de cada ângulo interno do polígono, basta dividir a soma dos ângulos internos pelo número de lados. Sendo assim, podemos encontrar a seguinte fórmula:
\(a_i = \frac{180\ \cdot \ {(n-2)}}{n}\)
ai: medida do ângulo interno.
- Exemplo: Qual é a medida de cada ângulo de um polígono regular de 12 lados?
Resolução:
Substituindo n = 12, temos que:
\(a_i = \frac{180\ \cdot \ {(12-2)}}{12}\)
\(a_i = \frac{180\ \cdot \ {(10)}}{12}\)
\(a_i = \frac{1800}{12}\)
\(a_i = 150°\)
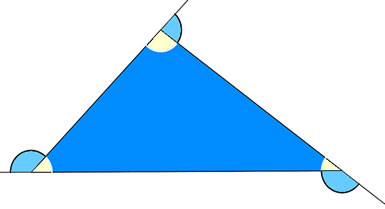
Agora, sobre os ângulos externos, para todo polígono (sendo ele regular ou não), a soma dos ângulos externos é igual a 360º. Então, como o polígono é regular, o valor de cada ângulo será dado por:
\(a_e = \frac{360}{n}\)
ae: ângulo externo.
n: número de lados.
- Exemplo: Qual é a medida do ângulo externo de um hexágono?
Resolução:
\(a_e = \frac{360}{6}\)
ae=60°
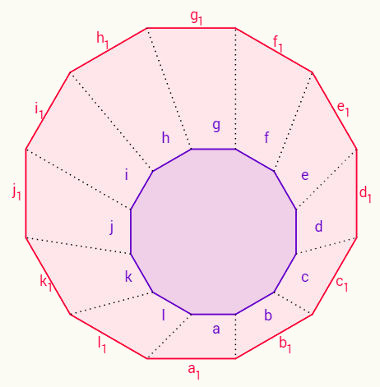
→ Apótema dos polígonos regulares
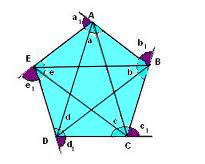
O apótema de um polígono regular é a medida do raio de uma circunferência circunscrita, sendo assim, o apótema vai do centro do polígono até um de seus lados de forma perpendicular.
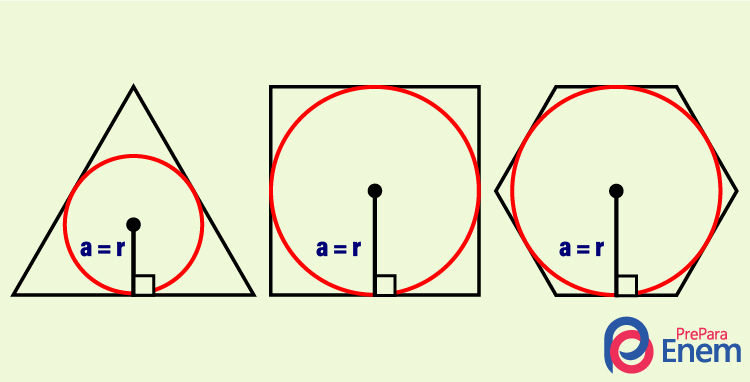
Observe na imagem acima que o apótema do polígono representado por a é igual ao raio da circunferência circunscrita.
→ Área do polígono regular
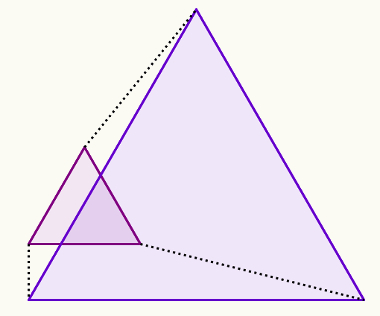
As fórmulas já existentes para os polígonos (por exemplo, para o triângulo, cujo cálculo da área é dado pelo produto da base pela altura) servem também para os polígonos regulares. Em específico, para os polígonos regulares, temos a fórmula que é o produto entre o apótema e o semiperímetro do polígono para calcular a área. O semiperímetro nada mais é que a metade do valor do perímetro do polígono.
\(A=a⋅p\)
a: apótema
p: semiperímetro (metade do comprimento do perímetro)
- Exemplo: Um octógono tem lados medindo 5 cm e apótema igual a 3,75 cm. Qual a sua área?
Resolução:
Sabemos que:
\(A=a⋅p\)
Calculando o perímetro, temos que:
\(P = 8 ⋅ 5 = 40\)
P = 40
Então temos que p = 20.
Logo, para calcular a área, temos que:
\(A = a ⋅ p\)
\(A = 3,75 ⋅ 20\)
A = 75cm2
Polígonos regulares x polígonos irregulares
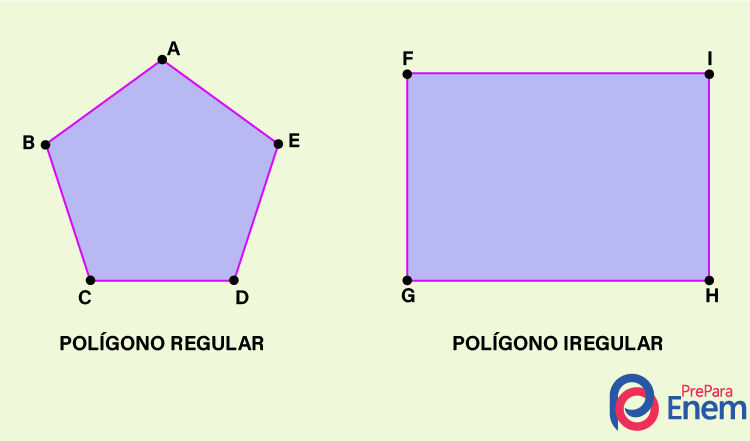
Como vimos, o polígono regular é o polígono que tem todos os lados congruentes e ângulos internos congruentes. Para que o polígono seja irregular, basta ele não satisfazer uma dessas condições, ou seja, não ser equilátero ou não ser equiângulo.
Saiba mais: O que são polígonos convexos?
Exercícios resolvidos sobre polígonos regulares
Questão 1
Um terreno tem formato de um hexágono regular. Para cercar esse terreno, serão utilizados 3 fios de arame farpado por lado. Nesse sentido, sabendo que a medida de um dos lados desse hexágono é 14 metros, então o total de arame farpado necessário é de:
A) 74 m
B) 128 m
C) 222 m
D) 236 m
Resolução:
Alternativa C
Primeiro calcularemos o perímetro:
\(P = 6 ⋅ 14 = 74m\)
Como será dada 3 voltas, então temos que:
\(74 ⋅ 3 = 222m \)
Questão 2
Qual é o valor de cada ângulo interno de um octógono regular?
A) 135º
B) 125º
C) 120º
D) 115º
E) 110º
Resolução:
Alternativa A
Sabemos que:
\(a_i = \frac {180 \cdot \ (n-2)}{n}\)
Então temos que:
\(a_i = \frac {180 \cdot \ (8\ -\ 2)}{8}\)
\(a_i = \frac {180\ \cdot \ 6}{8}\)
\(a_i = \frac {1080}{8}\)
\(a_i = 135°\)
Fontes
WAGNER E. Construções geométricas. (Coleção do Professor de Matemática). Rio de Janeiro: SBM, 1993.