Figuras congruentes são aquelas que possuem lados e ângulos correspondentes com medidas iguais. As medidas são iguais, mas os lados e ângulos não são. É como comparar paredes e ângulos de duas casas distintas. As medidas podem ser iguais, mas isso não quer dizer que as paredes da primeira casa sejam iguais às paredes da segunda. Imagine que a primeira casa é verde e a segunda é branca!
Do mesmo modo, não é possível afirmar que duas figuras congruentes são iguais. A igualdade entre elas é apenas entre as medidas de seus lados e de seus ângulos. Por isso, dizer que duas figuras são iguais significa dizer que a primeira figura é exatamente igual à segunda figura. Afirmar que duas figuras são congruentes é equivalente a dizer que a primeira figura possui medidas de ângulos e lados correspondentes de igual valor.
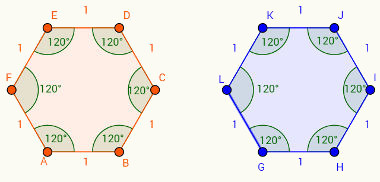
As duas figuras acima são congruentes por serem polígonos regulares de lado 1 cm e por possuírem todos os ângulos iguais a 120 graus, entretanto, a imagem seguinte torna a correspondência entre lados e ângulos mais óbvia.
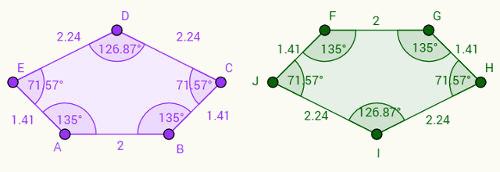
Imagine que o pentágono da direita é uma versão do pentágono da esquerda de cabeça para baixo. Observe que:
1- O lado AB é correspondente ao lado FG e que AB = FG = 2 cm.
2- O lado BC é correspondente ao lado GH e BC = GH = 1,41 cm.
3- Seguindo esse raciocínio, podemos escrever outros pares de lados congruentes: CD = IH, DE = IJ e EA = JF.
Com relação aos ângulos, observe que os ângulos correspondentes seguem o mesmo padrão dos lados. Por exemplo, o ângulo “a”, localizado no vértice A, é de 135 graus e é correspondente ao ângulo “f”, localizado no vértice F. Representando os ângulos pelos vértices correspondentes em letras minúsculas, teremos as correspondências: a = f, b = g, c = h, d = i, e = j.
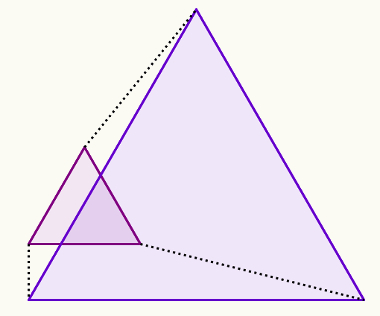
Existem figuras congruentes cujas medidas correspondentes não são tão óbvias. Repare na figura a seguir:
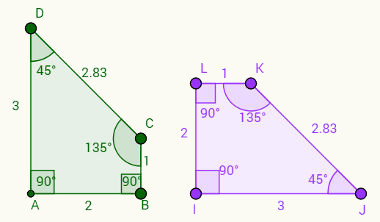
Observe que os ângulos correspondentes agora ocupam posições não tão óbvias quanto anteriormente. Observe as relações de congruência: a = i, d = j, c = k e b = l.
As relações de congruência entre os lados agora são as seguintes: AB = IL, BC = LK, CD = KJ e DA = IJ.
Portanto, duas figuras geométricas são congruentes quando as medidas de seus lados correspondentes são congruentes e, além disso, quando as medidas dos ângulos correspondentes são congruentes.