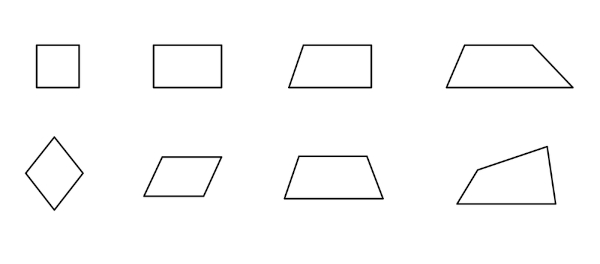
Os paralelogramos recebem esse nome por possuírem os lados opostos paralelos entre si. O paralelogramo é um polígono de quatro lados, estudado na geometria plana e com várias aplicações em exercícios que envolvem quadriláteros. Por definição, o paralelogramo é um quadrilátero que tem os lados opostos entre si, como:
Cada um desses polígonos é um caso particular de paralelogramo, e cada um deles possui fórmulas específicas para o cálculo de área e de perímetro. Devido as suas características, existem propriedades específicas dos paralelogramos relacionando seus ângulos e seus lados.
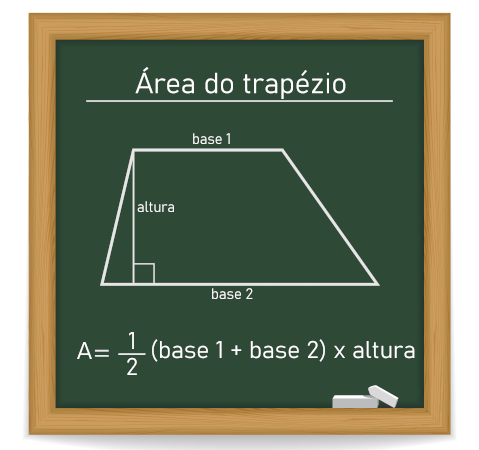
Leia também: Trapézio – quadrilátero que possui dois lados paralelos e dois lados não paralelos
Tópicos deste artigo
- 1 - Elementos de um paralelogramo
- 2 - Propriedades dos paralelogramos
- 3 - Qual é a área de um paralelogramo?
- 4 - Qual é o perímetro de um paralelogramo?
- 5 - Casos especiais de paralelogramo
- 6 - Exercícios resolvidos
Elementos de um paralelogramo
-
Lados paralelos
Para que um polígono seja um paralelogramo, deve ter os lados opostos paralelos:
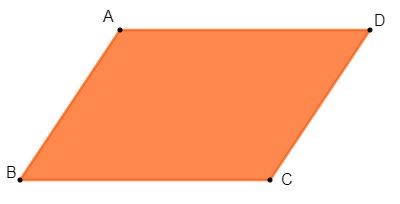
Os vértices são A, B, C e D, então AB, BC, CD e AD são os lados do paralelogramo, além disso, perceba que AB // DC e que AD // BC.
-
Soma dos ângulos
Por ser um quadrilátero, em todo paralelogramo, a soma dos ângulos internos é igual a 360º.
-
Diagonais
Todo paralelogramo possui duas diagonais.
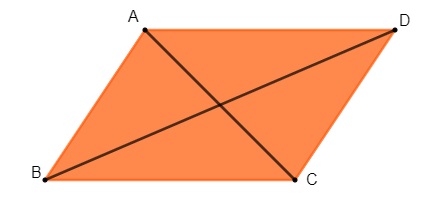
Os segmentos AC e BD são as diagonais desse paralelogramo.
Vale ressaltar que as características anteriores são todas herdadas pelo fato de o paralelogramo ser um quadrilátero, logo, todas elas se estendem para todos os polígonos que possuem quatro lados, porém existem propriedades exclusivas dos paralelogramos.
Propriedades dos paralelogramos
-
1ª propriedade: os lados opostos de um paralelogramo são congruentes.
Uma propriedade muito importante é a de que os lados opostos de um paralelogramo sempre têm a mesma medida, ou seja, são congruentes.
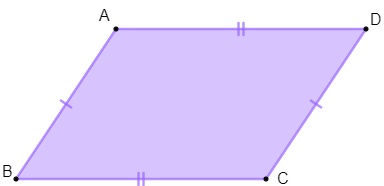
AB ≡ CD e AD ≡ BC
-
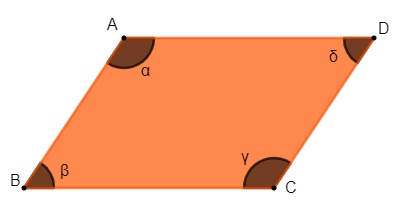
2ª propriedade: dois ângulos opostos em um paralelogramo são sempre congruentes.
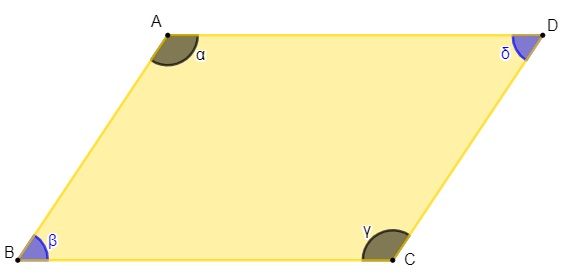
Α ≡ γ e δ ≡ β
-
3º propriedade: dois ângulos consecutivos de um paralelogramo são sempre suplementares.
Em um paralelogramo, dois ângulos consecutivos têm soma sempre igual a 180º, com base na imagem da propriedade anterior, temos que:
α + β = 180º
α + δ = 180º
δ + γ = 180º
β + γ = 180º
-
4ª propriedade: o ponto de encontro das duas diagonais é o ponto médio de cada uma delas.
Ao traçar as diagonais de um paralelogramo, o ponto de encontro entre elas divide-as ao meio.
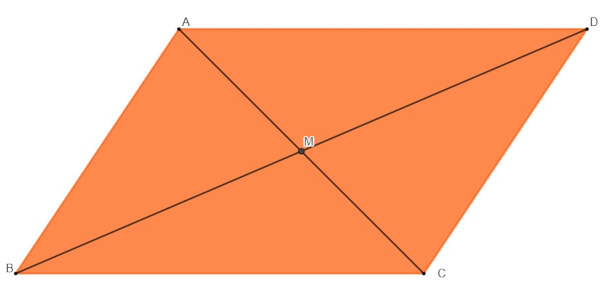
M é o ponto médio das diagonais.
Veja também: O que são polígonos semelhantes?
Qual é a área de um paralelogramo?
Para encontrar o valor da área de um paralelogramo, precisamos conhecer as dimensões da base e da altura desse polígono. Calcular a área nada mais é que encontrar o produto entre a base b e a altura h.
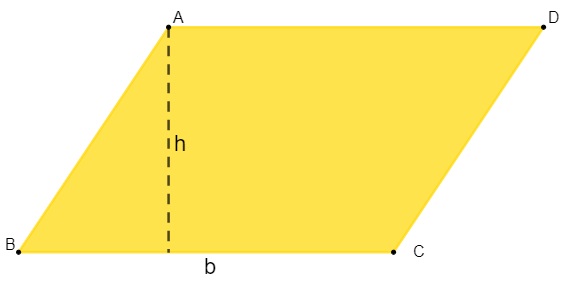
A = b x h
Qual é o perímetro de um paralelogramo?
Assim como todo polígono, para encontrar o perímetro de um paralelogramo, basta calcular a soma de todos os seus lados. Conhecendo os lados do paralelogramo, o perímetro é calculado por:
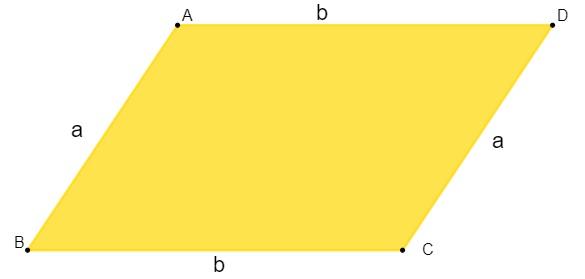
P = 2(a + b)
Exemplos:
Calcule a área e o perímetro do paralelogramo a seguir:
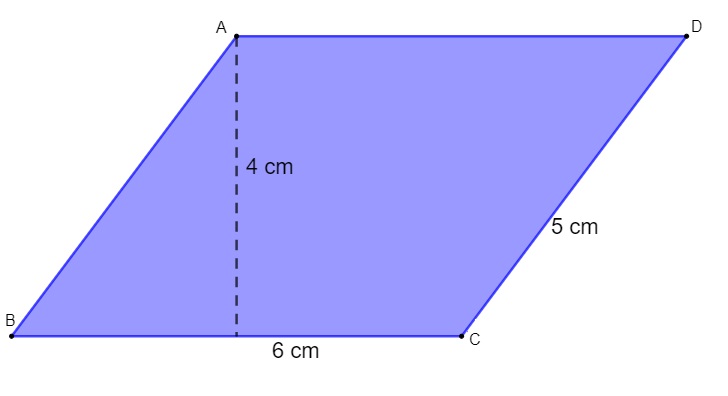
A = b × h
A = 6 × 4 = 24 cm²
Já o perímetro, temos que:
P = 2 (6 + 5) = 2 · 11 = 22 cm
Veja também: Congruência de figuras geométricas – quando figuras diferentes possuem mesmas medidas
Casos especiais de paralelogramo
Existem três casos particulares de paralelogramos, são eles o quadrado, o retângulo e o losango. Os três polígonos são paralelogramos importantes estudados como formas particulares.
-
Retângulo
Para ser classificado como um retângulo, o paralelogramo precisa ter todos os ângulos congruentes. Quando isso ocorre, todos os seus ângulos são de 90º, ou seja, retos, o que justifica o nome retângulo, que faz menção à medida dos ângulos. O detalhe é que, quando temos um retângulo, o lado que está na vertical coincide com a altura. A área pode ser encontrada com a multiplicação entre dois lados perpendiculares, e o perímetro é igual ao do paralelogramo.
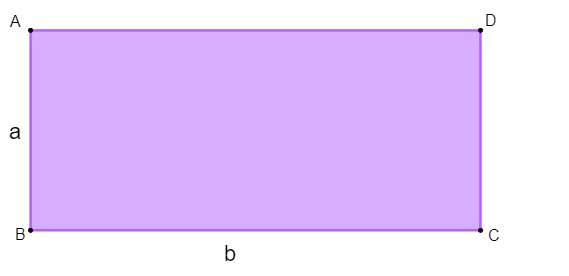
A = b × a
P = 2 (a + b)
-
Losango
Um paralelogramo é considerado um losango quando ele possui os quatro lados congruentes. Não há nenhuma restrição para os seus ângulos, podendo ser congruentes ou não. Para encontrar a área do losango, é necessário saber o valor da sua diagonal, já o perímetro é a soma dos quatro lados congruentes.
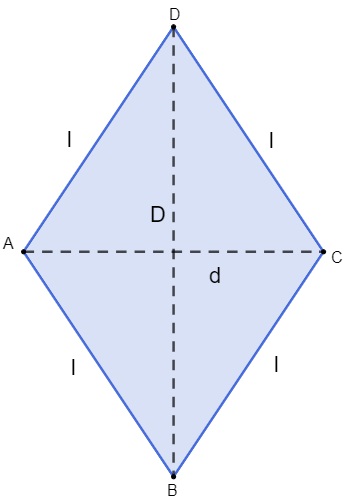
P = 4l
![]()
-
Quadrado
O quadrado é um paralelogramo que possui os quatro lados congruentes e os quatro ângulos retos, ou seja, todos os seus ângulos medem 90º. Ele pode ser considerado tanto um retângulo quanto um losango, e possui também as propriedades dos dois.
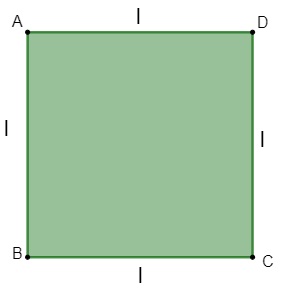
Como ele é um paralelogramo, para calcular a sua área, multiplicamos a base pela altura, e, para calcular o perímetro, somamos todos os lados do quadrado, nesse caso, temos que:
A = l²
P = 4l

Exercícios resolvidos
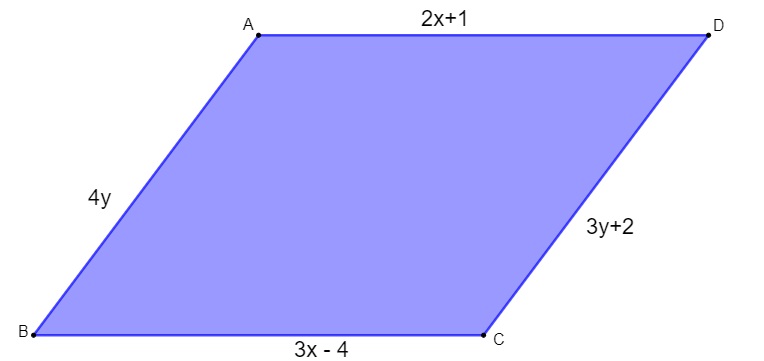
Questão 1 – Analisando o paralelogramo a seguir, o valor de x + y é:
A) 4
B) 5
C) 6
D) 7
E) 8
Resolução
Alternativa D
Como a figura é um paralelogramo, então os lados opostos são iguais, logo, temos que:
4y = 3y + 2
4y – 3y = 2
y = 2
Além disso:
3x – 4 = 2x + 1
3x – 2x = 1 + 4
x = 5
Então, x + y = 5 + 2 = 7
Questão 2 – Em um pátio de uma escola, o piso será todo substituído. Para calcular a quantidade de material que será utilizado, é importante conhecer a medida da área do pátio. Sabendo que esse pátio possui o formato de um paralelogramo com 4 metros de base e 5 metros de altura, então a área desse pátio é:
A) 10 m²
B) 100 m²
C) 200 m²
D) 20 m²
E) 15 m²
Resolução
Alternativa D
A = b × h
A = 4 × 5
A = 20 m²