Simetria é um princípio geométrico de correspondência entre formas. Há simetria quando um objeto pode ser divido em partes iguais, rotacionado ou deslocado sem alteração de sua estrutura original.
Os tipos de simetria são: de reflexão (ou axial), de rotação e de translação. Encontramos exemplos de simetria em expressões artísticas, construções arquitetônicas, plantas e animais.
Leia também: Figuras planas x figuras espaciais — qual a diferença?
Tópicos deste artigo
- 1 - Resumo sobre simetria
- 2 - O que é simetria?
- 3 - Quais são os tipos de simetria?
- 4 - Diferenças entre simetria e assimetria
- 5 - Qual é a importância da simetria?
- 6 - Exercícios resolvidos sobre simetria
Resumo sobre simetria
-
Se as partes de uma figura, quando sobrepostas, são coincidentes, então a figura é simétrica.
-
Existem três tipos principais de simetria: reflexão (ou axial), rotação e translação.
-
Um objeto é assimétrico quando não apresenta simetria.
O que é simetria?
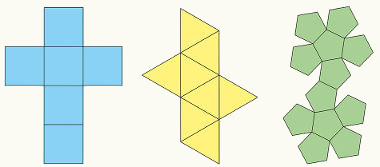
Simetria é quando uma figura pode ser dividida em partes que coincidem se sobrepostas. Considere a imagem abaixo. Perceba que se dobrarmos essa figura nos segmentos pontilhados, teremos quatro regiões sobrepostas coincidentes. Portanto, essa figura é simétrica.

Quais são os tipos de simetria?
O tipo de simetria mais conhecido é a simetria de reflexão (ou axial), mas também existe a de rotação e a de translação. Vamos conhecer cada uma.
-
Simetria de reflexão (ou axial)
A simetria de reflexão ocorre quando é possível desenhar uma ou mais retas que funcionam como um “espelho”, refletindo a imagem. Cada uma dessas retas é chamada de eixo de simetria.
Na figura a seguir, temos a metade esquerda do desenho de uma tulipa. Ao refletir essa imagem em torno do eixo vertical, construímos a tulipa colorida.

-
Simetria de rotação
A simetria de rotação acontece quando uma forma é rotacionada em torno de um ponto. Cada hélice de um cata-vento é obtida pela rotação de 90° da hélice anterior em torno do centro do cata-vento.

-
Simetria de translação
A simetria de translação se refere ao deslocamento de um objeto, sem alteração em sua forma. Na imagem abaixo, observamos a translação horizontal de dois tipos de triângulo.

Diferenças entre simetria e assimetria
Como o nome sugere, um objeto é assimétrico quando não apresenta nenhum tipo de simetria. Obras de arte e designs de interiores empregam elementos simétricos para produzir cenários harmônicos; já composições assimétricas podem ser utilizadas para transmitir personalidade.

Qual é a importância da simetria?
O uso de padrões simétricos em produções artísticas é uma prática recorrente em diferentes povos. Nesse contexto, a simetria integra uma forma de expressão cultural, conectada à visão de mundo de um grupo de pessoas.
Saiba mais: O que são polígonos semelhantes?
Exercícios resolvidos sobre simetria
Questão 1
(Enem) Um programa de edição de imagens possibilita transformar figuras em outras mais complexas. Deseja-se construir uma nova figura a partir da original. A nova figura deve apresentar simetria em relação ao ponto O.
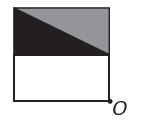
A imagem que representa a nova figura é:
a) 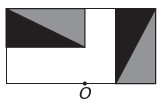
b) 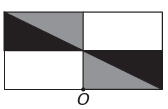
c) 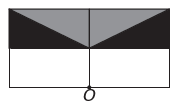
d) 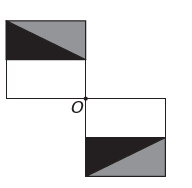
e) 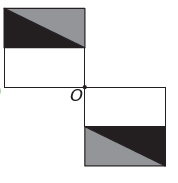
Resolução
Se a nova figura deve apresentar simetria em relação ao ponto O, então a figura original teve uma rotação em torno do ponto O. A única imagem em que isso acontece é
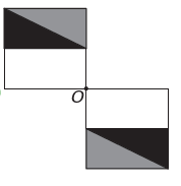
Note que a nova figura corresponde a uma rotação de 180° da figura original. Alternativa E.
Questão 2
(Uerj) Considerando o conceito de simetria, observe o desenho abaixo:
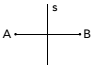
Os pontos A e B são simétricos em relação à reta s, quando s é a mediatriz do segmento AB. Observe este novo desenho:

Em relação à reta s, a imagem simétrica da letra R apresentada no desenho é:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Resolução
Note que a reta s é um eixo de simetria para a reflexão da letra R. Assim, a imagem simétrica da letra R em relação à reta s é
![]()
Alternativa C.
Créditos da imagem
Fontes
MENDES, I. A. Ensino de conceitos geométricos, medidas e simetria: por uma educação (etno)matemática com arte. Revista Cocar, Pará, v.2, n.4, p. (35-47), 2008. Disponível em: https://periodicos.uepa.br/index.php/cocar/article/view/105.
REZENDE, E.Q.F.; QUEIROZ, M. L. B. de. Geometria Euclidiana Plana: e construções geométricas. 2ª ed. Campinas: Unicamp, 2008.