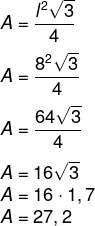O triângulo equilátero é um caso particular de triângulo estudado na geometria plana. Um triângulo é considerado equilátero quando ele possui todos os seus lados congruentes, ou seja, todos os lados têm a mesma medida. Quando um triângulo é equilátero, ele apresenta todas as propriedades de um triângulo qualquer e, além disso, apresenta algumas propriedades que são específicas do seu tipo.
O triângulo equilátero também possui todos os ângulos congruentes e, como a soma dos ângulos internos de um triângulo é sempre 180º, cada ângulo interno de um triângulo equilátero mede 60º. Para calcular a área e a altura de um triângulo equilátero, existem fórmulas específicas em que é necessário conhecer apenas a medida do lado desse triângulo.
Leia também: Qual é a condição de existência de um triângulo?
Tópicos deste artigo
- 1 - Propriedades do triângulo equilátero
- 2 - Altura do triângulo equilátero
- 3 - Área do triângulo equilátero
- 4 - Perímetro do triângulo equilátero
- 5 - Exercícios resolvidos
Propriedades do triângulo equilátero

O triângulo equilátero é um caso particular de triângulo estudado na geometria plana. O triângulo é um polígono que possui três lados e é classificado como equilátero quando ele tem todos os lados congruentes, ou seja, com a mesma medida.
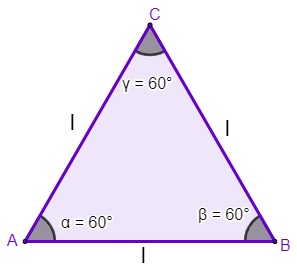
Como consequência dos lados congruentes, esse polígono também apresenta os seus três ângulos congruentes e, pelo fato de em triângulo qualquer a soma dos ângulos internos ser sempre igual a 180º, cada um dos ângulos internos de um triângulo equilátero é igual a 60º.
Ao traçarmos a altura de um triângulo equilátero, esse segmento de reta também será bissetriz do ângulo, dividindo o ângulo em duas partes iguais. A altura também é mediana, dividindo a base do triângulo em duas partes congruentes.
Altura do triângulo equilátero
Para calcular o valor da altura de um triângulo equilátero, utilizamos a seguinte fórmula:
![]()
Demonstração:
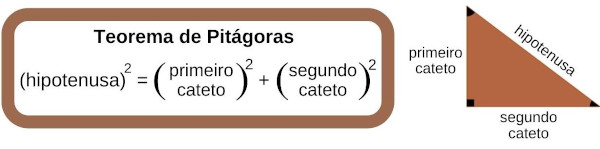
Ao traçarmos a altura, dividimos o triângulo equilátero em dois triângulos retângulos. Como a altura é mediana, a base vai ser dividida ao meio. Assim, podemos aplicar o teorema de Pitágoras nesse triângulo, isolando a altura.
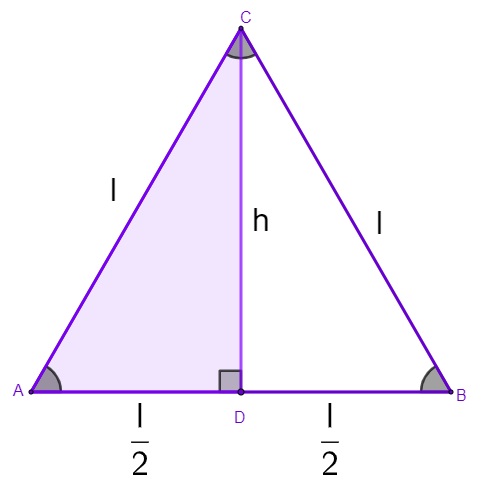
Analisando o triângulo destacado:
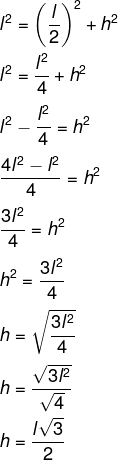
Exemplo 1:
Qual é a altura do triângulo equilátero cujo lado mede 20 cm?
Para encontrar o valor da altura desse triângulo equilátero, basta substituir na fórmula:
l = 20
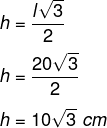
Exemplo 2:
Um triângulo equilátero possui altura igual a 12 cm. Qual é a medida do seu lado?
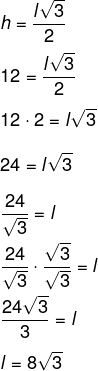
l = 8√3 cm
Veja também: Trapézio – quadrilátero que possui dois lados paralelos e dois lados não paralelos
Área do triângulo equilátero
A área de um triângulo, de uma maneira geral, é calculada a partir do produto da base pela altura dividido por 2. Quando analisamos, de forma específica, é possível deduzir uma fórmula que calcule a área do triângulo equilátero, tendo apenas a informação da medida do lado desse polígono.
A fórmula para calcular a área do triângulo equilátero é:
![]()
Demonstração:
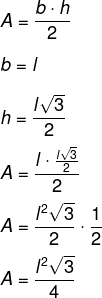
Exemplo:
Calcule a área de um triângulo retângulo que possui o lado igual a 10 cm.
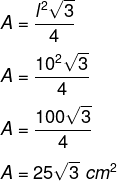
Perímetro do triângulo equilátero
O perímetro de qualquer polígono é igual à soma de todos os seus lados. Como os lados são congruentes, então o perímetro de um triângulo equilátero é dado por:
P = 3l
Exemplo:
Qual é o perímetro do triângulo equilátero que possui o lado medindo 8 cm?
P = 3l
P = 3·8
P = 24 cm
Veja também: O que são polígonos convexos?
Exercícios resolvidos
Questão 1 – Um triângulo equilátero possui lados medindo 2x + 10, y + 3 e 5x + 1. O valor de x + y é igual a:
A) 3
B) 8
C) 13
D) 15
E) 16
Resolução
Alternativa E.
Por ser um triângulo equilátero, então os lados são congruentes.
Logo:
2x + 10 = 5x + 1
2x – 5x = 1 – 10
– 3x = – 9 ( – 1)
3x = 9
x = 9/3
x = 3
Sendo x = 3, então o lado do triângulo é:
l = 2x + 10
l = 2·3+10
l = 6 + 10
l = 16
Para encontrar o valor de y, sabemos que:
y+3 = 16
y = 16 – 3
y = 13
Agora calculando o valor de x + y :
13 + 3 = 16
Questão 2 – A área, em metros quadrados, limitada por um triângulo equilátero com lados medindo 8 metros é igual a:
(Use √3 = 1,7)
A) 27,2
B) 25,3
C) 24,8
D) 21,1
E) 16,0
Resolução
Alternativa A.
Para encontrar a área, basta substituir os valores dados na fórmula: