As provas de Matemática geralmente exigem que o estudante recorde-se de algum conhecimento específico para interpretar as questões. Alguns conseguem se sair bem nessa etapa de resolução, mas tem dificuldades em conceitos mais básicos, como multiplicação e divisão. Pensando nisso, reunimos três macetes matemáticos para facilitar os estudos e agilizar os cálculos nas questões do Enem.
Além disso, também existem aquelas fórmulas, propriedades e conceitos difíceis de memorizar. Dois deles serão citados adiante, mas adiantamos que formas criativas de memorização, como uma música, poesia, mapa mental etc., funcionam e recomendamos a utilização delas.
Leia também: Dicas de Matemática para o Enem
Tópicos deste artigo
Primeiro macete: Multiplicação
O primeiro macete envolve multiplicação e não será possível ser mais breve do que seremos nos próximos parágrafos.
-
Multiplicação por potências de 10
Lembre-se de que as potências de 10 são 100 = 102, 1000 = 103...
Sempre que um número for multiplicado por uma potência de 10, utilizaremos um dos dois raciocínios a seguir:
1. Se for um número decimal, a vírgula andará n casas para a direita (n é o número de zeros da potência de 10 ou o expoente dessa potência). Observe que, se sobrarem casas não preenchidas nesse processo, deveremos ocupá-las com zeros. Por exemplo:
1000·2,2 = 2200,0 ou 2200
Note que a vírgula andou três casas para a direita, deixando alguns espaços desocupados, que foram preenchidos com zeros.
2. Se não for um número decimal, ao final dele, adicione n zeros (n é o número de zeros da potência de 10 ou seu expoente). Por exemplo:
10000·45 = 450000
Sem realizar cálculo algum, descobrimos o resultado, pois colocamos os zeros de 10000 ao final de 45.
-
Multiplicação por múltiplos de 10
Para resolvê-la, proceda da seguinte maneira: repare que, ao final, todo múltiplo de 10 possui alguns zeros. Ignore-os na multiplicação e coloque-os no resultado final, seguindo o raciocínio do macete anterior. Observe o exemplo:
235·45000
235·45 = 10575
Logo: 235000·45 = 10575000
-
Propriedades da multiplicação
Existe uma propriedade da multiplicação que facilita tanto os cálculos que, após algum tempo, é utilizada para efetuar multiplicações de cabeça: a propriedade distributiva da multiplicação.
Para usá-la, lembre-se de que todo número maior que 1 pode ser decomposto em uma soma de números inteiros. Por exemplo, 22 = 20 + 2. Ora, não é mais fácil multiplicar um número qualquer por 2 e por 20 (utilizando o primeiro macete) do que por 22? Observe:
205·22 = 205·(20 + 2)
205·20 = 4100
205·2 = 410, então:
205·22 = 205·(20 + 2) = 4100 + 410 = 4510
Veja também: Temas de matemática que mais caem no Enem

Segundo macete: Áreas
Quase todas as áreas de figuras geométricas baseiam-se na área do paralelogramo. Assim, para ajudar a memorizar as fórmulas, tente lembrar a área dessa figura geométrica, que é:
A = b·h
b: base
h: altura
A área do quadrado é exatamente igual a essa, mas às vezes aparece com outra forma, em razão de o quadrado possuir todos os lados iguais. Desse modo, sua altura será igual a l, assim como sua base. Segue que a área do quadrado é:
A = l·l = l2
A área do triângulo sempre será metade da área do paralelogramo, pois todo triângulo é exatamente metade de um paralelogramo. Logo, a sua área poderá ser obtida pela divisão da área do paralelogramo por 2:
A = b·h
2
A área do trapézio, por sua vez, é obtida pela soma de suas bases, mas a fórmula é igual à da área do triângulo. Pense no trapézio como sendo um corte de um triângulo ou um triângulo com duas bases (embora esse último não exista). A fórmula da área do trapézio é a seguinte:
A = (B + b)·h
2
Terceiro macete: Trigonometria
Pensando naqueles que sempre se esquecem da tabela dos valores de seno, cosseno e tangente dos ângulos notáveis, vamos construí-la de uma forma diferente. Veja a canção (infelizmente não podemos cantar) seguinte:
“um, dois, três.
Três, dois, um.
Tudo sobre dois,
só não tem raiz o um”
Agora, construindo a tabela enquanto cantamos:
“Um, dois, três. Três, dois, um”:
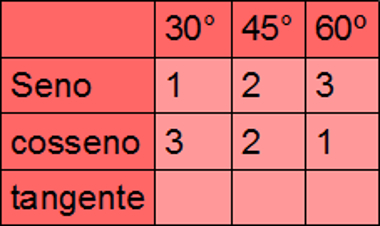
“Tudo sobre dois”:
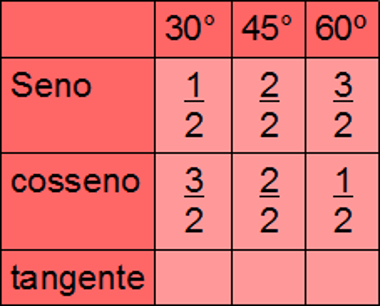
“Só não tem raiz o um”:
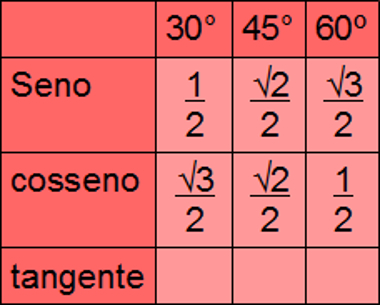
A tangente, por sua vez, é resultado da divisão de seno por cosseno. Para encontrar seus valores, lembre-se de que, na divisão de frações, multiplicamos a primeira pelo inverso da segunda. Se necessário, fazemos a racionalização do resultado.