Quando nos deparamos com um triângulo equilátero, temos a certeza de que se trata também de um triângulo equiângulo, pois os três ângulos são iguais. Sabendo que a soma dos ângulos de um triângulo qualquer é 180°, podemos chamar os ângulos de nosso triângulo por x. Sendo assim:
x + x + x = 180°
3x = 180°
x = 180°
3
x = 60°
Portanto, podemos concluir que os ângulos de nosso triângulo equilátero são iguais a 60°. Se traçarmos a bissetriz de um dos ângulos e também a altura do mesmo lado, veremos que elas coincidem, isto é, por se tratar de uma bissetriz, ela dividirá um ângulo de 60° ao meio e formará um ângulo de 90° com o lado oposto ao ângulo, podendo essa reta ser classificada como altura. Haverá a formação de dois triângulos idênticos. Realizando a análise de um desses, veremos que é um triângulo formado pelos ângulos 30°, 60° e 90°. Se traçarmos a bissetriz referente ao ângulo de 90°, formaremos um novo triângulo, agora com um ângulo de 45°. Esses ângulos destacados são chamados de ângulos notáveis. O processo descrito para encontrar esses ângulos pode ser visualizado na figura a seguir:
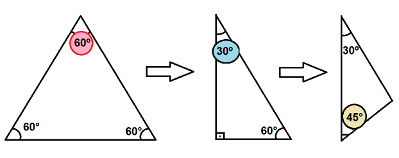
Procedimento para verificar quais são os ângulos notáveis
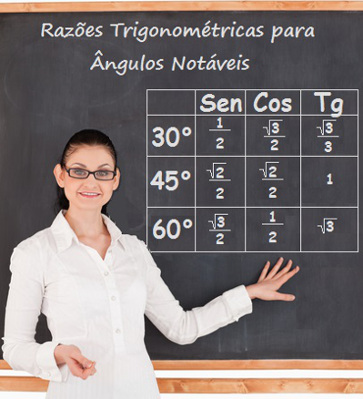
Ao trabalharmos com exercícios sobre trigonometria, vamos nos deparar com diversas questões que exigem conhecimento acerca das razões trigonométricas (seno, cosseno e tangente) de ângulos notáveis. A partir delas, podemos encontrar as razões trigonométricas de outros ângulos. Vamos começar o processo de montagem da tabela de razões trigonométricas dos ângulos notáveis:
1°) Organize a tabela! Nos elementos da primeira linha, coloque as razões trigonométricas:
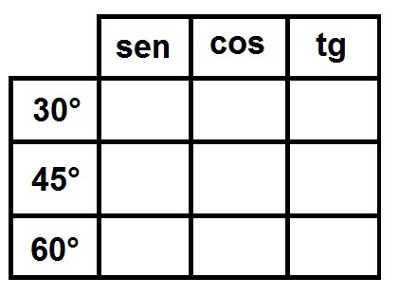
Organizando a tabela de razões trigonométricas para os ângulos notáveis
2°) Desce e Sobe! Agora, preenchemos a coluna do seno de cima para baixo e a do cosseno de baixo para cima com a sequência numérica 1, 2, 3. A tabela ficará da seguinte forma:
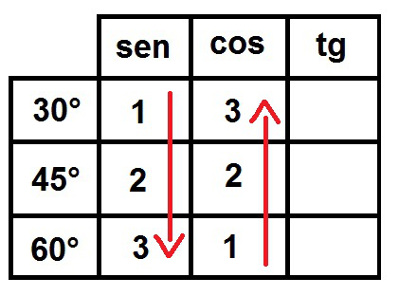
Começando a preencher as colunas de seno e cosseno
3°) Olhe a raiz! Nós vamos agora preencher o símbolo da raiz para todos os números, exceto para o 1. Feito isso, escrevemos todos esses números como frações, de modo que todos tenham denominador igual a dois. Vejamos como ficará:
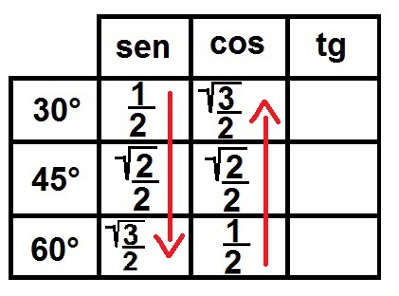
Concluindo as razões seno e cosseno para os ângulos notáveis
4°) Tudo muda na Tangente! Na coluna da tangente, a regra muda. Nós usaremos o sentido de cima para baixo. Para preencher, devemos colocar “raiz de três sobre três, um e raiz de três.” Assim sendo:
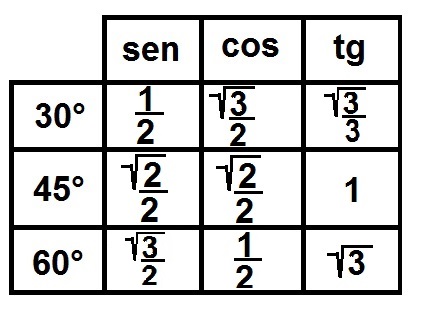
Finalmente preenchemos a tangente em nossa tabela de razões trigonométricas
Pronto, agora você já sabe como montar a tabela de razões trigonométricas! Sempre que for resolver exercícios de trigonometria, faça um esboço dessa tabela em seu caderno, pois, certamente, você precisará dela.
Aproveite para conferir nossa videoaula sobre o assunto: