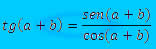A origem da trigonometria está diretamente relacionada à astronomia, uma vez que as necessidades humanas contribuíram significativamente para a busca de meios de produção agrícola. Para produzir alimento, tornou-se necessário o conhecimento dos astros, das estações do ano, do movimento da Terra, e foi exatamente nesse momento que a matemática demonstrou suas contribuições. A matemática é uma ciência que busca modelar a realidade em fórmulas, estruturas e padrões, graças a essa ciência conseguimos transcrever a realidade numericamente e geometricamente.
Os babilônios e os egípcios já estudavam e utilizavam a trigonometria na Antiguidade, mas foi no período helênico que o estudo relacionado a essa área das ciências exatas ganhou maior notoriedade. Esses estudos foram motivados em razão da necessidade de se ter um maior rigor relacionado ao conceito da medida de ângulo.
Na Grécia, Hipócrates e Eudoxo foram personalidades importantes que estudaram conceitos relacionados à medição de ângulo. Hipócrates, que foi considerado o pai da trigonometria, foi o responsável pelos estudos relacionados às propriedades das cordas envolvendo os ângulos inscritos em círculos, ele também criou o que podemos considerar como a primeira tabela trigonométrica; já Eudoxo realizou o estudo relacionado à medição de ângulo para calcular o tamanho da Terra. Mesmo com tantos estudos relacionados à trigonometria, ainda não se tinha o devido rigor matemático.
Euclides e Arquimedes conseguiram, em seus estudos, evidenciar de forma mais clara o que viria a ser a trigonometria que utilizamos nos dias de hoje. Nos estudos realizados por ambos é possível identificar fórmulas equivalentes às razões trigonométricas, ou seja, seno, cosseno e tangente.
Sysntaxis mathematica (Almajesto), escrita por Ptolomeu de Alexandria, foi a obra mais significativa para os estudos de trigonometria, que relacionou ângulos centrais com cordas de um círculo.
Os árabes, os persas e os hindus também contribuíram para a criação da trigonometria. Podemos atribuir maior relevância aos estudiosos: AL Battani, Aryabhata e Abu'l Wafa.
Mesmo a trigonometria tendo toda essa origem histórica, estudos apontam que a sua formulação com o rigor do qual utilizamos hoje data do século XVII, sendo possível graças ao desenvolvimento da álgebra. Veja outros nomes importantes:
-
Fibonacci foi tido como um dos matemáticos que, inicialmente, mais contribuiu para trigonometria no século XVII, em virtude de sua obra Practica Geometriae, que foi um estudo da trigonometria árabe com a agrimensura.
-
O matemático Purbach, no século XIV, elaborou uma nova tábua de seno, baseando-se nos estudos de Ptolomeu.
-
Regiomontanus foi considerado um dos maiores matemáticos do século XV, ele foi o autor do livro Tratado sobre triângulos, discípulo de Purbach, foi quem conseguiu emancipar a trigonometria em relação à astronomia, seu livro continha a trigonometria completa.
-
Pitiscus foi quem criou a palavra trigonometria, esse termo apareceu pela primeira vez em um de seus livros.
Não pare agora... Tem mais depois da publicidade ;) -
John Newton publicou o Tratado da Trigonometria Britannica, livro baseado nos estudos de Gellibrand, que foi considerado o mais completo livro tratando dos assuntos relacionados à trigonometria do seu tempo.
-
John Wallis também contribuiu muito, pois conseguiu expressar fórmulas trigonométricas sem utilizar proporções.
A trigonometria ganhou a configuração que possui nos dias de hoje depois do estudioso matemático Euler, que adotou o raio como medida de unidade do círculo.
Foi possível observar que a trigonometria foi constituída por diversos povos e cada um, em um determinado período da história, fez a diferença para a construção dessa parte das ciências exatas.
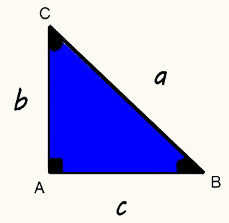
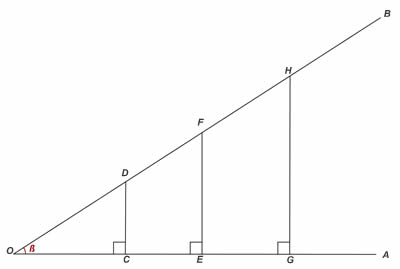
A trigonometria é caracterizada como um estudo que relaciona lados e ângulos de um triângulo retângulo. Dessa relação advém as razões trigonométricas: seno, cosseno e tangente. Sendo:
-
Seno - a razão entre o cateto oposto ao ângulo e a hipotenusa.
sen B = b cateto oposto
a hipotenusa
-
Cosseno - a razão entre o cateto adjacente ao ângulo e a hipotenusa.
cos B = c cateto adjacente
a hipotenusa -
Tangente - a razão entre o cateto oposto ao ângulo e o cateto adjacente a esse mesmo ângulo.
tg B = b cateto oposto
c cateto adjacente
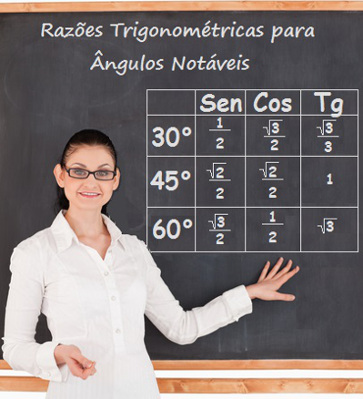
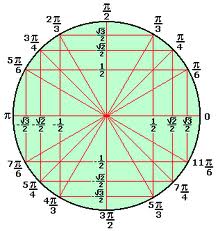
Como critério fundamental de ângulos para triângulo temos que a soma dos ângulos internos do triângulo deve ser 180 graus. Diante disso, quando falamos de ângulos no triângulo, eles podem ser do tipo notáveis ou não. Os ângulos notáveis são os de 30º, 45º e 60º, independente de ser ângulo notável ou não todos estão representados na Tábua trigonométrica. Essa tábua tem o formato de tabela e possui o valor dos ângulos 0º a 90º, o que corresponde a um quarto do ciclo trigonométrico. Para cada valor de ângulo da tábua temos os respectivos valores equivalentes ao seno, cosseno e tangente. A tabela de ângulos notáveis pode ser construída a partir da tábua trigonométrica, observe a imagem abaixo:

A trigonometria é uma área de estudo das ciências exatas e abrange as seguintes subáreas.
-
Razões trigonométricas e Relações entre as razões;
-
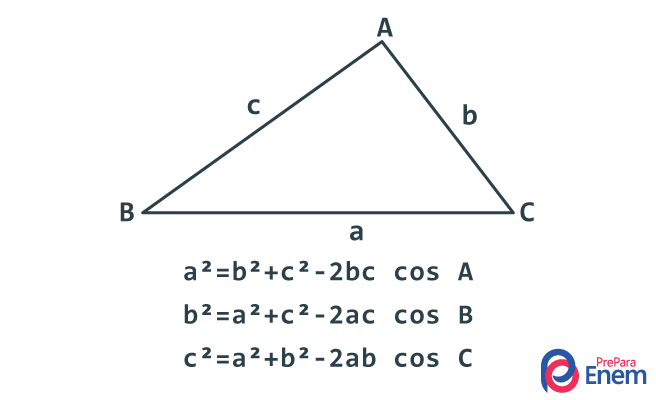
Ralações métricas no triângulo;
-
Circunferência, quadrante e funções circulares;
-
Trigonometria do triângulo retângulo e Relações trigonométricas;
-
Equações e inequações trigonométricas;
-
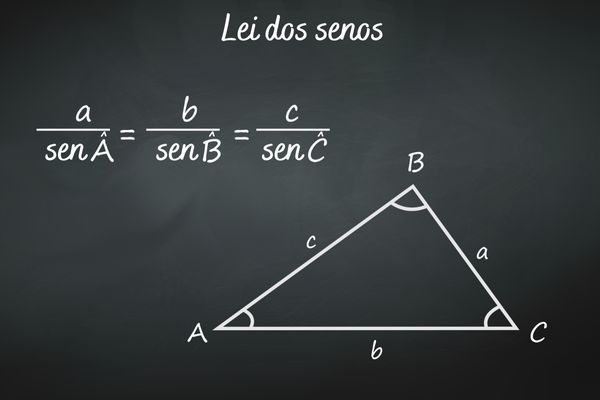
Resolução de triângulo.
As aplicações relacionadas à trigonometria não estão restritas somente à matemática, está presente: na física, na cartografia, na arquitetura, na medicina, na engenharia entre muitas outras. Graças à trigonometria, mudamos e reformulamos a forma como manipulamos, calculamos e mensuramos polígonos e formas circulares.