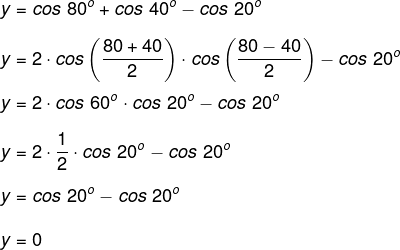Transformações trigonométricas

Transformações trigonométricas são fórmulas utilizadas com o objetivo de facilitar o cálculo do valor de uma razão trigonométrica, seno, cosseno ou tangente, por meio de uma transformação, que muitas vezes converte o ângulo em um ângulo notável, ou seja, aquele em que o valor do seno, do cosseno ou da tangente é conhecido. As principais transformações trigonométricas são:

• a soma e a diferença entre arcos;

• fórmulas para arco duplo;

• transformações em produtos.

Leia também: Relações fundamentais da trigonometria

Tópicos deste artigo

• 1 - Resumo sobre transformações trigonométricas
• 2 - O que são as transformações trigonométricas?
  • Videoaula sobre razões trigonométricas
• 3 - Quais são as fórmulas de transformações trigonométricas?
  • Soma de dois arcos
  • Diferença de dois arcos
  • Arcos duplos
  • Arco metade
  • Transformação em produto
• 4 - Exercícios resolvidos sobre transformações trigonométricas

Resumo sobre transformações trigonométricas

• As transformações trigonométricas são fórmulas que auxiliam no cálculo das razões trigonométricas.

• As principais transformações trigonométricas são:

  • soma de dois arcos;

  • diferença de dois arcos;

  • arco duplo;

  • arco metade;

  • transformação em produto.

O que são as transformações trigonométricas?

Chamamos de transformações trigonométricas as fórmulas que utilizamos para transformar uma razão trigonométrica em outra em que seja mais fácil calcular o valor do seno, do cosseno e da tangente. Geralmente, quando utilizamos as transformações trigonométricas, dispomos de um ângulo que não é notável e o transformamos em um ângulo notável.

Os ângulos notáveis são aqueles de 30°, 45° e 60°. Entretanto, também é conveniente transformar a razão trigonométrica em um ângulo de 0°, 90°, 180°, 270° ou 360°, cujos valores do seno, cosseno e tangente são fáceis de encontrar. É o caso, também, dos ângulos simétricos aos ângulos notáveis nos demais quadrantes, como os ângulos de 120°, 135°, 150°, 210°, 225°, 240°, 300°, 315° e 330°, os quais possuem valor de seno, cosseno e tangente fáceis de encontrar.

Já para os demais ângulos, quando o valor da razão trigonométrica não é conhecida, lança-se mão das transformações trigonométricas, com o objetivo de encontrar um dos ângulos citados para facilitar o cálculo.

• Videoaula sobre razões trigonométricas

Quais são as fórmulas de transformações trigonométricas?

As principais transformações trigonométricas são: soma de dois arcos, diferença de dois arcos, arco duplo, arco metade e transformação em produto. A seguir, veja cada caso em detalhes.

• Soma de dois arcos

Na soma de dois arcos, há uma fórmula para o seno, uma para o cosseno e uma para a tangente:

• • Seno da soma: sen(a + b) = sen(a) · cos(b) + sen(b) · cos(a)

  • Cosseno da soma: cos(a + b) = cos(a) · cos(b) – sen(a) · sen(b)

  • Tangente da soma:

Exemplo:

Calcule o cos(105°).

Resolução:

O ângulo de 105° não é um ângulo notável, mas sabemos que 105 = 45 + 60. É conveniente utilizar a fórmula do cosseno da soma, já que os ângulos de 45° e 60° são notáveis. Dessa forma, obtém-se o seguinte:

cos(45° + 60°) = cos 45° ⸳ cos 60° – sen 45° · sen 60°

Substituindo as razões trigonométricas pelos seus respectivos valores, temos que:

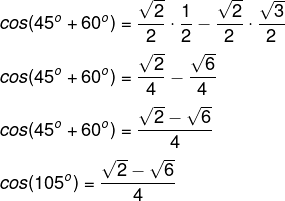
• Diferença de dois arcos

  • Seno da diferença: sen(a – b) = sen(a) · cos(b) – sen(b) · cos(a)

  • Cosseno da diferença: cos(a – b) = cos(a) · cos(b) + sen(a) · sen(b)

  • Tangente da diferença:

Exemplo:

Calcule o valor do sen(15°).

Resolução:

Sabemos que 15° = 45° – 30°, então podemos reescrever essa razão trigonométrica como a diferença entre dois arcos e utilizar a transformação para encontrar sua solução.

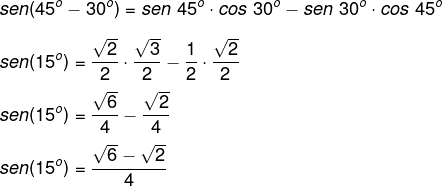
• Arcos duplos

As fórmulas dos arcos duplos nada mais são que aplicações das fórmulas da soma de dois arcos para dois arcos congruentes.

• • Seno do arco duplo: sen(2a) = 2sen(a) · cos(a)

  • Cosseno do arco duplo: cos(2a) = cos(a)² – sen(a)²

  • Tangente do arco duplo:

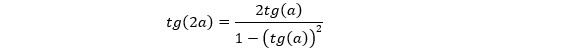
Exemplo:

Sabendo que sen(a) = 0,9 e cos(a) = 0,4, qual o valor de cos(2a)?

Resolução:

Sabemos que cos(2a) = cos(a)² – sen(a)²:

cos(2a) = 0,4² – 0,9²

cos(2a) = 0,16 – 0,81

cos(2a) = – 0,65

• Arco metade

Além do arco duplo, existe também uma transformação para quando divide-se o arco por dois.

• • Cosseno do arco metade:

• • Seno do arco metade:

• • Tangente do arco metade:

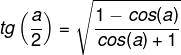
Exemplo:

Encontre o valor da tangente de um ângulo de 15°.

Resolução:

Sabemos que 15° = 30 : 2. Como o ângulo de 30° é notável, tem-se o seguinte:

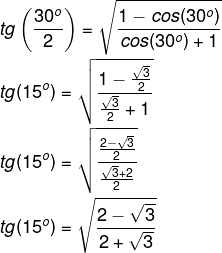
• Transformação em produto

É possível, também, transformar as razões trigonométricas em produto, o que em alguns casos pode facilitar o cálculo da expressão. Veja, a seguir, as principais transformações em produto.

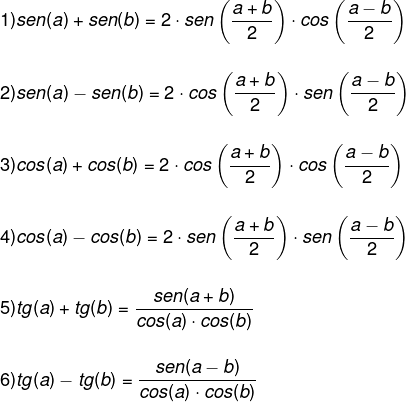
Leia também: Equações trigonométricas — aquelas que apresentam uma razão trigonométrica

Exercícios resolvidos sobre transformações trigonométricas

Questão 1

(Unifenas) Sendo dados sen(x) = 0,8 e cos(x) = 0,6, qual é o valor do sen(2x)?

A) 0,96

B) 0,90

C) 0,80

D) 0,70

E) 0,60

Resolução:

Alternativa A

Utilizando a fórmula do arco duplo:

sen(2x) = 2sen(x) · cos(x)

Substituindo os valores conhecidos:

sen(2x) = 2 · 0,8 · 0,6

sen(2x) = 0,96

Questão 2

(Mack-SP — adaptada) Qual o valor simplificado da expressão y = cos 80° + cos 40° – cos 20°?

A) 0

B) 1

C) 2

D) 3

E) 4

Resolução:

Alternativa A

Primeiramente, utilizaremos a transformação em produto de cos 80° + cos 40°. Dessa forma, calcula-se: