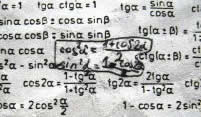As relações fundamentais da trigonometria são igualdades por meio das quais é possível relacionar as razões trigonométricas básicas: seno, cosseno e tangente. São duas as relações fundamentais que recebem esse nome graças a seu envolvimento em grande parte das fórmulas e cálculos da trigonometria intermediária.
As duas relações fundamentais da trigonometria são:
tgα = senα
cosα
e:
sen2α + cos2α = 1
Cada uma dessas relações será demonstrada a seguir, mas, antes, é preciso conhecer algumas informações sobre o ciclo trigonométrico.
Ciclo trigonométrico
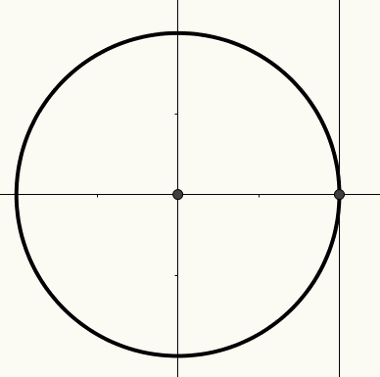
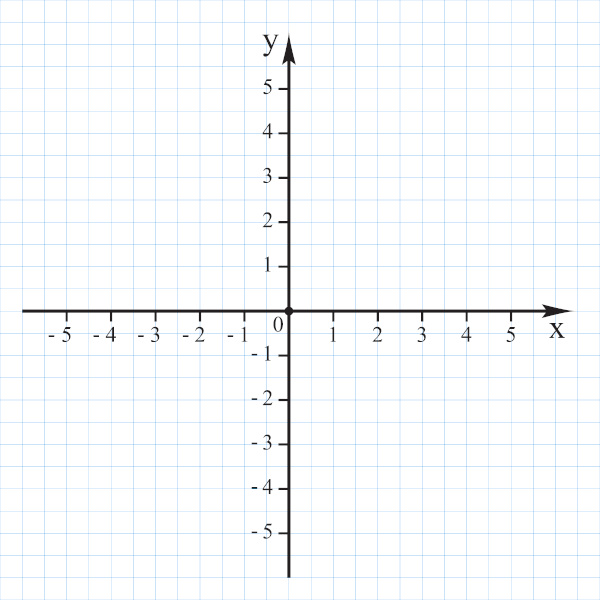
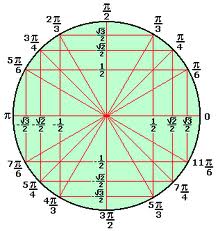
O ciclo trigonométrico é uma circunferência de raio 1 e centro (0, 0) construída no plano cartesiano. Sobre essa circunferência é possível construir arcos, que, por sua vez, relacionam-se a ângulos. Arcos e ângulos relacionam-se a uma medida de comprimento obtida no eixo x, no eixo y ou no eixo das tangentes.
O eixo x é conhecido como eixo dos cossenos, o eixo y é conhecido como eixo dos senos e a terceira reta, presente na figura a seguir, é conhecida como eixo das tangentes.
Para obter mair informações a respeito do ciclo e do modo como ângulos devem ser relacionados a números reais e a medidas de razões trigonométricas, leia o artigo Ciclo trigonométrico.
Demonstração da primeira relação
No ciclo trigonométrico, marque o ponto P, trace o segmento de reta que liga o eixo das tangentes ao centro do ciclo, que deve ser o vértice de qualquer ângulo construído, formando assim o ângulo α.
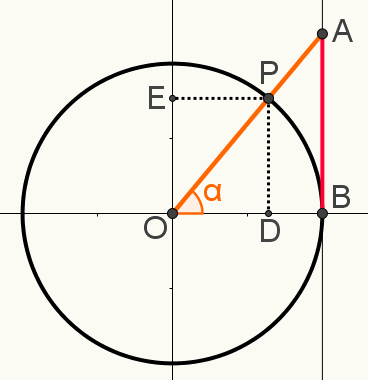
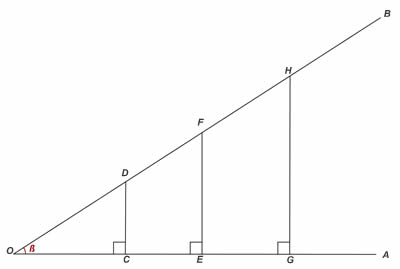
Ainda nessa construção, assinale os prolongamentos do ponto P sobre o eixo dos senos e dos cossenos, respectivamente os pontos E e D. A imagem a seguir mostra a construção final usada para determinar uma das relações trigonométricas:
Observe que os triângulos OAB e OPD são semelhantes. Isso significa que as medidas de seus lados são proporcionais. Isso acontece porque ambos são triângulos retângulos, e, além do ângulo reto, compartilham o ângulo α. Portanto, pelo caso ângulo-ângulo, eles são considerados semelhantes.
Sendo assim, é possível escrever a seguinte proporção:
AB = OB
PD OD
Perceba que o segmento OD é igual a cosα; que o segmento PD é igual a senα; que o segmento OB = 1, pois é raio da circunferência; e que o segmento AB = tgα. Substituindo esses valores na proporção acima, e simplificando o resultado, teremos:
tgα = senα
1 cosα
tgα = senα
cosα
Essa é, portanto, a demonstração da primeira relação fundamental.
Segunda relação fundamental
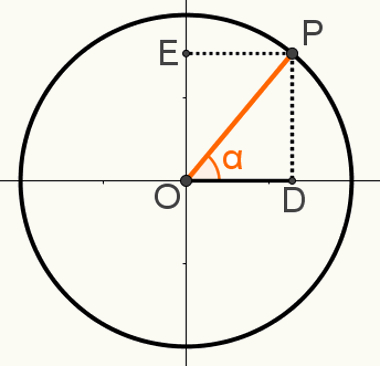
Para demonstrar a segunda relação fundamental, construa um ponto P sobre o ciclo, de modo que o segmento OP seja um de seus raios. Observe o ângulo α resultante na imagem a seguir:
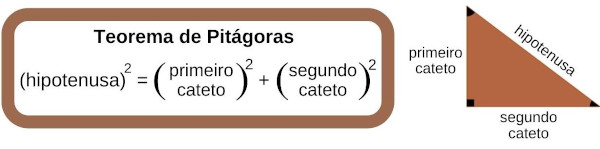
O triângulo retângulo OPD é formado nessa construção. Sabendo que a medida OP = 1, porque esse segmento é um raio do círculo, que OD = cosα e que PD = senα, podemos usar o teorema de Pitágoras para:
OP2 = OD2 + PD2
12 = cosα2 + senα2
Ou seja:
cosα2 + senα2 = 12
Ambas as demonstrações dependem de conhecer previamente o ciclo trigonométrico. Conhecendo-o, é possível perceber que elas são fáceis e que não dependem de cálculos avançados.
Aproveite para conferir nossas videoaulas sobre o assunto: