Seno e Cosseno de dois ângulos suplementares

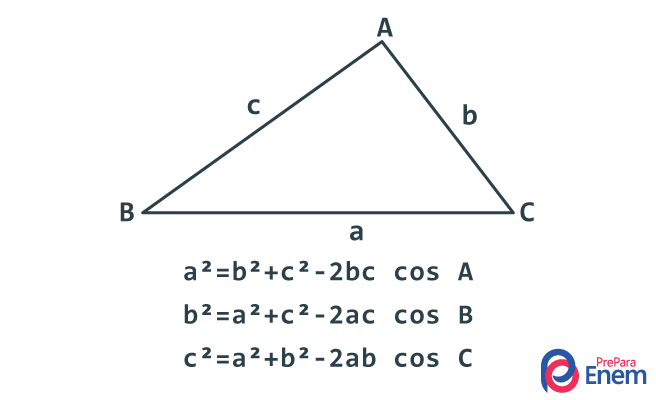
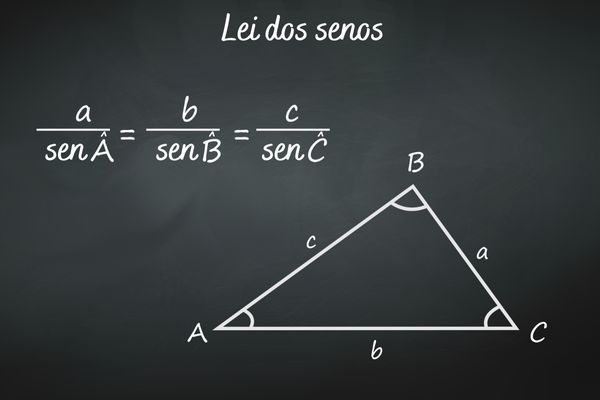
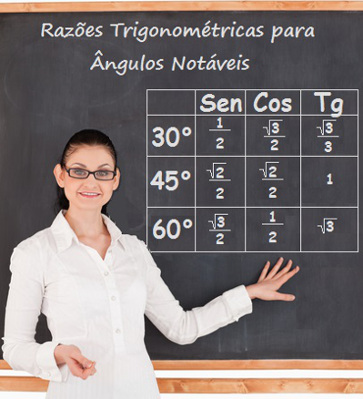
Em geral, ao trabalharmos com trigonometria, lembramos logo do triângulo retângulo. Mesmo que o professor se esqueça de marcar o ângulo reto, sempre surge uma pergunta: Professor, aquele ali é o ângulo de 90°? Mas se não há um triângulo retângulo, ainda podemos falar em trigonometria? Sim, podemos! Existem relações trigonométricas que são aplicadas apenas a triângulos obtusângulos, aqueles em que algum dos ângulos é maior do que 90°. Para esse tipo de triângulo, temos importantes relações que nos permitem identificar valores de seno e cosseno de ângulos suplementares. Mas antes de aprofundarmos, vamos relembrar a definição de ângulos suplementares:

“Dois ou mais ângulos são ditos suplementares se a soma de suas medidas é igual a 180°.”

Portanto, se temos o ângulo 20°, o seu suplemento é dado por 180° – 20° = 160°. Para o ângulo 110°, o suplemento é dado por 180° – 110° = 70°. Também é o caso de um ângulo x, o suplemento é dado por 180° – x.

Observe o seguinte triângulo obtusângulo:

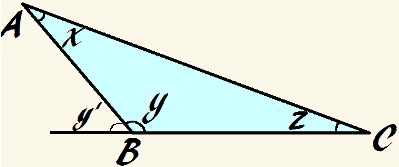
Nesse triângulo, o ângulo y é obtuso e x + y + z = 180°

Como em qualquer triângulo, se somarmos os ângulos internos, teremos:

x + y + z = 180°

Se o ângulo y é obtuso, ele é maior do que 90° e, portanto, a soma dos demais ângulos deve ser menor do que 90°:

x + z < 90°

Podemos dizer ainda que x, y e z são suplementares, pois sua soma é 180°. Então, como nos exemplos anteriores, podemos definir que:

y = 180° – (x + z)

Utilizando um princípio básico de ângulo externo, podemos ainda afirmar que o ângulo externo a y, na imagem denominado por y', equivale à soma dos ângulos internos do triângulo não adjacentes a si, portanto:

y' = x + z

Logo, podemos afirmar que y' é suplementar ao ângulo y. Portanto, podemos afirmar novamente que:

y = 180° – y'

Vamos agora estabelecer as relações de seno e cosseno para esses ângulos suplementares. Dado um ângulo y qualquer e seu suplemento 180 – y, temos as seguintes relações:

sen (180° – y) = sen y

cos (180° – y) = – cos y

Essas relações só não são válidas se considerarmos y = 90°. Vejamos algumas situações em que podemos empregar as relações acima.

1. Sendo o sen (30°) = ½ , determine o sen (150°):

Nesse caso, o ângulo y em questão é 30°, então

sen (180° – y) = sen y

sen (180° – 30°) = sen (30°)

sen (150°) = sen (30°)

sen (150°) = ½

Portanto, o seno de 150° é ½.

2. Sendo o cos (30°) = √2 , determine o cos (150°):
                                  2

   Nesse caso, o ângulo y em questão é 30°, então

   cos (180° – y) = – cos y

   cos (180° – 30°) = – cos (30°)

   cos (150°) = – cos (30°)

   cos (150°) = – √3
                         2

   Portanto, o seno de 150° é – √2 .
                                              2