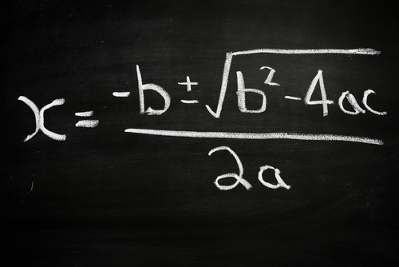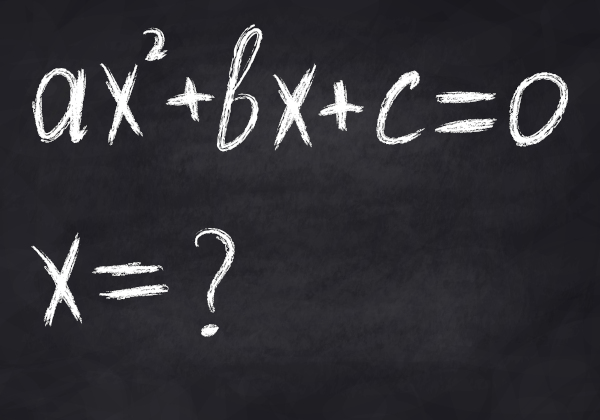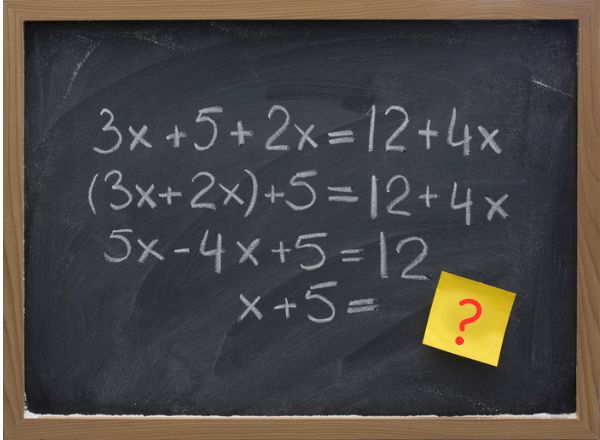Equações são expressões algébricas que possuem uma igualdade. Essas expressões são chamadas de algébricas porque possuem pelo menos uma incógnita, que é um número desconhecido representado por uma letra. As inequações, por sua vez, são relações semelhantes às equações, contudo, apresentam uma desigualdade.
Enquanto as equações relacionam os termos do primeiro membro aos termos do segundo, afirmando sua igualdade, as inequações mostram que os termos do primeiro membro são maiores ou menores que os elementos do segundo.
Termos de uma equação e de uma inequação
Termo é o nome que se dá ao produto de algum número por alguma letra. Para identificá-los, basta procurar pelas multiplicações separadas por sinais de adição ou subtração. Veja a equação seguinte:
4x + 2x – 7x = 16 – 5x
Os termos são: 4x, 2x, – 7x, 16 e – 5x
Membros de uma equação e de uma inequação
Primeiro e segundo membros são definidos pela igualdade nas equações e pela desigualdade nas inequações.
Todos os termos dispostos à esquerda da igualdade ou da desigualdade compõem o primeiro membro de uma equação ou inequação. Todos os termos dispostos à direta da igualdade ou desigualdade determinam o segundo membro de uma equação ou inequação.
Desse modo, dada a inequação:
2x + x – 9x ≤ 15 – 4x
Os termos 2x, x e –9x pertencem ao primeiro membro, e os termos 15 e – 4x pertencem ao segundo.
O que é igualdade e desigualdade?
Ambos determinam relações de ordem entre números e incógnitas. O sinal de igual é utilizado quando se quer expressar a seguinte situação: Existe um valor para as incógnitas que faz com que o resultado dos cálculos propostos no primeiro membro seja igual ao resultado dos cálculos propostos no segundo.
A desigualdade, por sua vez, pode ser representada por um dos quatro símbolos seguintes:
<, >, ≥ e ≤
Esses símbolos mostram que o conjunto de operações do primeiro membro possui um resultado “menor”, “maior”, “maior igual” ou “menor igual” ao resultado do segundo membro.
Grau
O grau de equações e de inequações pode ser encontrado da seguinte maneira:
Se a equação ou a inequação possui apenas uma incógnita, então, o grau dela é dado pelo maior expoente da incógnita. Por exemplo: o grau da equação 4x3 + 2x2 = 7 é 3.
Se a equação ou inequação possui mais de uma incógnita, então, o grau dela é dado pela maior soma entre os expoentes de um mesmo termo. Por exemplo, o grau da equação 4xyz + 7yz2 – 5x2y2z2 = 0 é 6.
Exemplos de equações:
1) 4x = 16
2) 2x – 8 = 144
3) 18x2 = 2x – 8
x
Exemplos de inequações:
1) 12x + x2 ≤ 12
2) 144 ≥ 12x + 7
3) 128 – 14x < 12x + 4