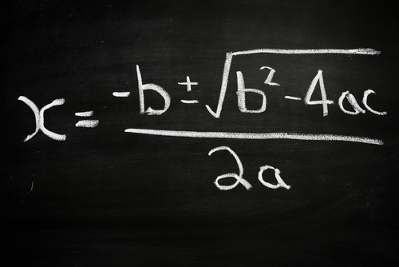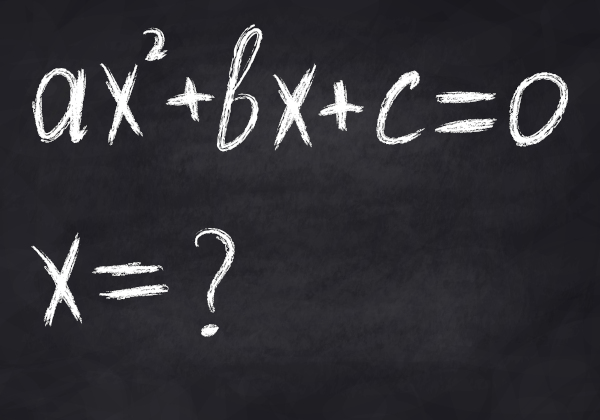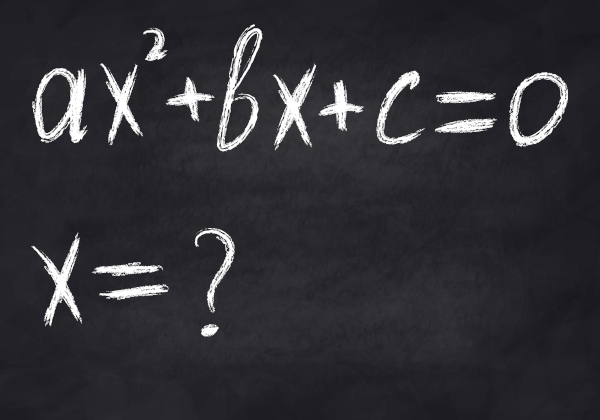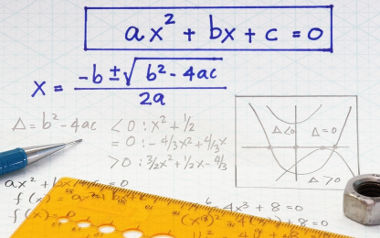A fórmula de Bhaskara é um método resolutivo para equações do segundo grau. Tendo os coeficientes da equação em mãos, basta substituí-los na fórmula e realizar os cálculos para encontrar seus resultados.
É bom ter em mente que os resultados de uma equação são os valores de x que tornam aquela equação verdadeira. A equação 2x = 16, por exemplo, tem apenas um resultado: x = 8. Esse resultado é justamente o número que, multiplicado por 2, tem como resultado 16.
Tópicos deste artigo
O que é uma equação do segundo grau?
Uma equação do segundo grau é uma expressão algébrica que apresenta uma igualdade e uma incógnita elevada ao quadrado ou o produto entre duas incógnitas.
Uma equação de grau 1 possui uma incógnita elevada à primeira potência; uma equação do grau 2 possui uma incógnita elevada à segunda potência e assim sucessivamente. A quantidade de resultados de uma equação é igual ao seu grau, ou seja, uma equação de grau 2 possui 2 resultados, que, às vezes, podem não ser números reais. Nesse caso, dizemos que a equação não possui solução ou não possui resultados reais.
Fórmula de Bhaskara
Para resolver uma equação do segundo grau utilizando a fórmula de Bhaskara, essa equação necessariamente deve estar escrita da seguinte forma:
![]()
Estando nesse formato, pode-se utilizar o seguinte passo a passo para resolver equações do segundo grau:
Passo 1 – Separar coeficientes
Observe que o coeficiente “a” é o número que multiplica a incógnita “x2”; o coeficiente “b” é o número que multiplica “x”, e o coeficiente “c” é o número fixo, isto é, o número que não multiplica incógnita alguma.
Passo 2 – Calcular o discriminante
O cálculo do discriminante deve ser realizado da seguinte maneira: substitua os valores numéricos dos coeficientes que foram separados na fórmula do discriminante e realize as operações indicadas pela fórmula.
O discriminante é representado pela letra grega Δ (delta), e a fórmula para calculá-lo é a seguinte:
![]()
Passo 3 – Calcular as raízes, resultados ou valores de x
Raízes, resultados ou valores de x referem-se à mesma coisa, isto é, aos dois resultados da equação do segundo grau. Para tanto, utiliza-se a fórmula de Bhaskara da seguinte maneira: substitua nela os valores numéricos dos coeficientes e de Δ e faça os cálculos indicados pela fórmula, ilustrada na imagem a seguir:
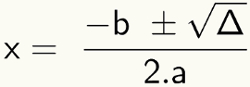
Observação: Note que, nesse passo, é utilizado o símbolo “±” antes de √Δ. Esse símbolo apenas quer dizer que x deve ser calculado duas vezes, uma para + √Δ e outra para – √Δ.
Exemplo:
Resolva a equação x2 + 8x – 9 = 0.
Passo 1: separaremos os coeficientes dessa equação. O coeficiente a = 1, pois x2 não está sendo multiplicado por número algum, e b = 8 e c = – 9.
Passo 2: Calculamos o discriminante utilizando a fórmula abaixo:
Δ = b2 – 4·a·c
Δ = 82 – 4·1·(– 9)
Δ = 64 + 36
Δ = 100
Passo 3: Calculamos os valores de x utilizando a fórmula de Bhaskara:
x = – b ± √Δ
2·a
x = – 8 ± √100
2·1
x = – 8 ± 10
2
Observe agora que é necessário fazer um cálculo para + 10 e outro para – 10:
x' = – 8 + 10
2
x' = 2
2
x' = 1
e
x'' = – 8 – 10
2
x'' = – 18
2
x'' = – 9
Aproveite para conferir nossas videoaulas relacionadas o assunto: