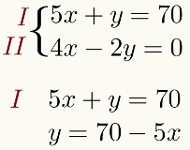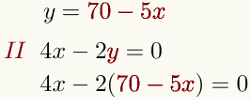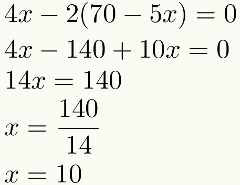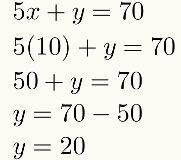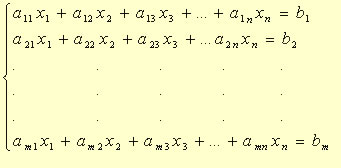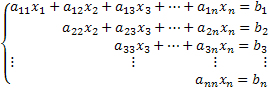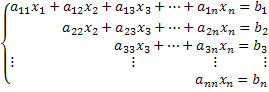Os sistemas lineares são conjuntos de equações nas quais as mesmas incógnitas representam os mesmos números. Por exemplo, nas equações 2x + y = 10 e 3x + y = 12, x = 2 e y = 6 para ambas, por isso, podemos dizer que elas formam um sistema. Geralmente, as equações desse tipo relacionam-se a situações cotidianas, e exercícios envolvendo sistemas lineares são frequentemente abordados em vestibulares e no Enem. Para resolver esses sistemas, ou seja, encontrar os valores das suas incógnitas, existem alguns métodos.
Neste artigo, discutiremos o método da substituição em etapas para facilitar o aprendizado. Para ensinar as etapas de resolução de um sistema com duas equações e duas incógnitas, usaremos o seguinte exemplo:
1ª Etapa: isolar uma incógnita
A primeira etapa para resolver esse sistema consiste em escolher uma incógnita, aquela que for mais oportuna, em uma das duas equações e descobrir seu valor algébrico. Isso significa fazer as operações necessárias para deixar essa incógnita sozinha em um dos membros da equação.
A incógnita que, ao ser isolada, torna os cálculos mais fáceis, é sempre aquela cujo coeficiente é 1. Assim, no sistema linear, não deve aparecer nenhum número multiplicando essa incógnita. No exemplo dado, isolaremos a incógnita y da primeira equação. Nesse caso, temos:
Observe que, para isolar a incógnita y da primeira equação, bastou trocar 5x de membro. Como 5x estava positivo, passou para o outro lado negativo.
2ª Etapa: realizar a substituição
Nesse etapa, substituímos o valor algébrico encontrado na equação que ainda não foi usada. Em outras palavras, como descobrimos o valor algébrico de y usando a primeira equação, substituiremos esse valor na segunda.
Caso tivéssemos descoberto o valor algébrico de y usando a segunda equação (na primeira etapa), substituiríamos esse valor na primeira e essa regra também valeria para outras incógnitas.
Substituir o valor de uma incógnita em uma equação é tarefa simples: onde essa incógnita aparecer, coloque o valor dela entre parêntesis. Observe:
3ª Etapa: realizar os cálculos
Note que, após a substituição, restará apenas uma incógnita na segunda equação nesse exemplo. Isso significa que sempre teremos uma equação com uma incógnita nessa terceira etapa. Resolvendo essa equação, encontramos o valor de uma das incógnitas. Observe:
Encontrado o valor numérico de uma das incógnitas, realizaremos a quarta e última etapa:
4ª Etapa: encontrar o valor da segunda incógnita
Para realizar essa etapa, basta substituir o valor numérico encontrado na etapa anterior em qualquer uma das duas equações. No exemplo, substituiremos o valor de x na primeira equação, observe:
Aproveite para conferir nossa videoaula sobre o assunto: