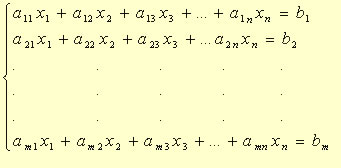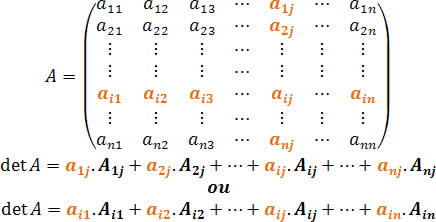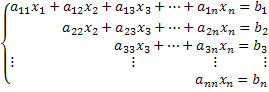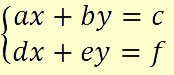A regra de Cramer é uma ferramenta matemática usada para resolver sistemas lineares que apresentam a mesma quantidade de equações e incógnitas. Para utilizar esse método, é necessário utilizar a representação matricial do sistema e calcular alguns determinantes.
Leia também: Escalonamento — um método para classificar, resolver e discutir sistemas lineares de qualquer ordem
Tópicos deste artigo
- 1 - Resumo sobre a regra de Cramer
- 2 - O que é a regra de Cramer?
- 3 - Como se usa a regra de Cramer?
- 4 - Exercícios resolvidos sobre regra de Cramer
Resumo sobre a regra de Cramer
-
A regra de Cramer é um método para resolver sistemas lineares.
-
Esse método é válido para sistemas possíveis e determinados, ou seja, que possuem apenas um conjunto solução.
-
Em um sistema possível e determinado, o determinante da matriz dos coeficientes é diferente de zero.
-
Para um sistema 2x2, se D é a matriz dos coeficientes, Dx é a matriz obtida ao substituir a coluna dos coeficientes de x pelos termos independentes e Dy é a matriz obtida ao substituir a coluna dos coeficientes de t pelos termos independentes. Então, de acordo com a regra de Cramer:
\(x=\frac{D_x}{D}\) e \(y=\frac{D_y}D\)
O que é a regra de Cramer?
A regra de Cramer é um método para resolver um sistema linear formado por n equações e n incógnitas. Lembre-se que resolver um sistema linear (conjunto de equações lineares que estão relacionadas) significa encontrar o valor de cada uma das incógnitas.
Para que essa técnica seja válida, é necessário que a matriz formada pelos coeficientes das incógnitas tenha determinante não nulo. Isso garante que o sistema é possível e determinado, isto é, que possui apenas um conjunto solução.
Vamos conhecer a regra de Cramer para o seguinte sistema:
\( \left \{ \begin{matrix} a_1 x+b_1 y=c_1 \\a_1 x+b_1 y=c_1 \end{matrix} \right. \)
Considere a matriz dos coeficientes (também chamada de matriz incompleta do sistema):
\(A= \begin{bmatrix} a_1 & b_1 \\ a_2 & b_2 \end{bmatrix}\)
Se \(det\ A≠0\), então, segundo a regra de Cramer, a solução do sistema é
\(x=\frac{D_x}D\)
\(y=\frac{D_y}D\)
-
D → determinante da matriz A (matriz dos coeficientes).
-
Dx → determinante da matriz obtida ao substituir em A a coluna dos coeficientes de x pelos termos independentes do lado direito da igualdade.
-
Dy → determinante da matriz obtida ao substituir em A a coluna dos coeficientes de y pelos termos independentes do lado direito da igualdade.
Ou seja,
\(D= \begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}\) , \(D_x= \begin{vmatrix} c_1 & b_1 \\ c_2 & b_2 \end{vmatrix}\) e \(D_y= \begin{vmatrix} a_1 & c_1 \\ a_2 & c_2 \end{vmatrix}\)
Como se usa a regra de Cramer?
Para utilizar a regra de Cramer, devemos calcular os determinantes necessários e obter os valores das incógnitas.
-
Exemplo:
Utilizando a regra de Cramer, encontre o conjunto solução do sistema
\( \left \{ \begin{matrix} 3x+y=9 \\x+4y=14 \end{matrix} \right. \)
Resolução:
Note que o determinante da matriz dos coeficientes não é nulo:
\(D= \begin{vmatrix} 3 & 1 \\ 1 & 4 \end{vmatrix}=11\)
Assim, a regra de Cramer é válida. Portanto,
\(x=\frac{D_x}D\) e \(y=\frac{D_y}D\)
Agora, basta encontrar Dx e Dy:
\(D_x= \begin{vmatrix} 9 & 1 \\ 14 & 4 \end{vmatrix}=22\)
\(D_y= \begin{vmatrix} 3 & 9 \\ 1 & 14 \end{vmatrix}=33\)
Logo,
\(x=\frac{D_x}D=\frac{22}{11}=2\)
\(y=\frac{D_y}D=\frac{33}{11}=3\)
O conjunto solução do sistema é S = {2,3}.
→ Solução de sistemas lineares usando a regra de Cramer
◦ Solução de sistema 2x2 usando a regra de Cramer
Vejamos outro exemplo de uso da regra de Cramer para resolver um sistema 2x2. Utilizando a regra de Cramer, vamos determinar o conjunto solução do sistema a seguir:
\( \left \{ \begin{matrix} 2x+3y=16 \\-3x+7y=45 \end{matrix} \right. \)
Perceba que o determinante da matriz dos coeficientes não é nulo:
\(D= \begin{vmatrix} 2 & 3 \\ -3 & 7 \end{vmatrix}=11\)
Portanto, a regra de Cramer é válida. Assim,
\(x=\frac{D_x}D\) e \(y=\frac{D_y}D\)
Agora, basta encontrar Dx e Dy:
\(D_x= \begin{vmatrix} 16 & 3 \\ 45 & 7 \end{vmatrix}=-23\)
\(D_y= \begin{vmatrix} 2 & 16 \\ -3 & 45 \end{vmatrix}=138\)
Logo,
\(x=\frac{D_x}D=\frac{-23}{23}=-1\)
\(y=\frac{D_y}{D}=\frac{138}{23}=6\)
O conjunto solução do sistema é S = {-1,6}.
◦ Solução de sistema 3x3 usando a regra de Cramer
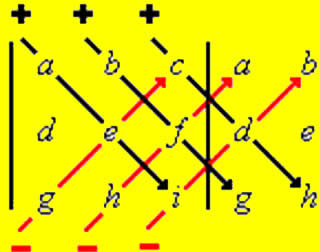
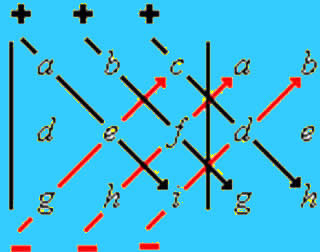
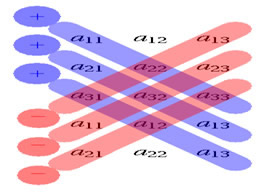
No caso de um sistema 3x3, devemos considerar que todas as matrizes e determinantes envolvidos possuem 3 linhas e 3 colunas. Assim, é necessário conhecer técnicas para obter o determinante de uma matriz 3x3, como a regra de Sarrus.
Utilizando a regra de Cramer, vamos determinar o conjunto solução do sistema a seguir:
\( \left \{ \begin{matrix} x+2y+z=12 \\2x+3y-z = 6 \\ 3x+y+2z=16 \end{matrix} \right. \)
Perceba que agora buscamos os valores de x, y e z.
Note que o determinante da matriz dos coeficientes não é nulo:
\(D= \begin{vmatrix} 1 & 2 & 1 \\ 2 & 3 & -1 \\ 3 & 1 & 2 \end{vmatrix}=-14\)
Portanto, a regra de Cramer é válida. Assim,
\(x=\frac{D_x}D\), \(y=\frac{D_y}D\) e \(z=\frac{D_z}D\)
\(D_x= \begin{vmatrix} 12 & 2 & 1 \\ 6 & 3 & -1 \\ 16 & 1 & 2 \end{vmatrix}=-14\)
\(D_y= \begin{vmatrix} 1 & 12 & 1 \\ 2 & 6 & -1 \\ 3 & 16 & 2 \end{vmatrix}=-42\)
\(D_z= \begin{vmatrix} 1 & 2 & 12 \\ 2 & 3 & 6 \\ 3 & 1 & 16 \end{vmatrix}=-70\)
Logo,
\(x=\frac{D_x}D=\frac{-14}{-14}=1\)
\(y=\frac{D_y}D=\frac{-42}{-14}=3\)
\(z=\frac{D_z}D=\frac{-70}{-14}=5\)
O conjunto solução do sistema é S = {1,3,5}.
◦ Solução de sistema 4x4 usando a regra de Cramer
Para resolver sistemas 4x4 pela regra de Cramer, é necessário conhecer técnicas para o cálculo de determinantes de matrizes com 4 linhas e 4 colunas, como o teorema de Laplace. O princípio é o mesmo que o utilizado para os sistemas menores.
Se x, y, z e w são as incógnitas de um sistema 4x4, então, pela regra de Cramer,
\(x=\frac{D_x}D\), \( y=\frac{D_y}D\), \(z=\frac{D_z}D\) e \(w=\frac{D_w}D\)
Veja também: Método da substituição para solução de sistemas lineares com duas equações
Exercícios resolvidos sobre regra de Cramer
Questão 1
Considere as afirmações abaixo.
I. A regra de Cramer é válida para matrizes 3x2.
II. Em um sistema quadrado, o determinante da matriz dos coeficientes deve ser diferente de zero para que a regra de Cramer possa ser aplicada.
III. Não há relação entre a regra de Cramer e o cálculo de determinantes.
Está correto o que se afirma em
A) I, apenas.
B) II, apenas.
C) I e III, apenas.
D) II e III, apenas.
E) III e IV, apenas.
Resolução:
Alternativa B.
I. A regra de Cramer é válida para matrizes 3x2. (falsa)
A regra de Cramer é válida apenas para matrizes quadradas.
II. Em um sistema quadrado, o determinante da matriz dos coeficientes deve ser diferente de zero para que a regra de Cramer possa ser aplicada. (verdadeira)
III. Não há relação entre a regra de Cramer e o cálculo de determinantes. (falsa)
O uso da regra de Cramer está relacionado ao cálculo de determinantes.
Questão 2
O conjunto solução do sistema \( \left \{ \begin{matrix} x-y=6 \\2x+3y=22 \end{matrix} \right. \) é
A) S = {5, 2}
B) S = {5,10}
C) S = {8, 2}
D) S = {8,10}
E) S = {8,40}
Resolução:
Alternativa C.
O determinante D da matriz dos coeficientes é
\(D= \begin{vmatrix} 1 & -1 \\ 2 & 3 \end{vmatrix}=5\)
Os determinantes Dx e Dy são
\(D_x= \begin{vmatrix} 6 & -1 \\ 22 & 3 \end{vmatrix}=40\)
\(D_y= \begin{vmatrix} 1 & 6 \\ 2 & 22 \end{vmatrix}=10\)
Assim,
\(x=\frac{D_x}D=\frac{40}5=8\)
\(y=\frac{D_y}D=\frac{10}5=2\)