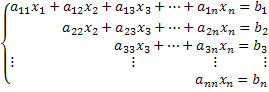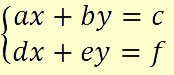Classificação de sistemas lineares escalonados

Para classificarmos um sistema linear que esteja escalonado, temos apenas que analisar a última linha do sistema, caso o sistema esteja completamente escalonado. Caso a quantidade de linhas não corresponda à quantidade de incógnitas, ou seja, caso existam incógnitas que não serão escalonadas, denominaremos estes sistemas “sistemas incompletos” e completaremos as demais linhas da seguinte forma: 

Sistemas incompletos são resolvidos de uma maneira diferenciada e sua classificação é dada como um sistema possível indeterminado. Fato este que pode ser compreendido pelo cálculo do determinante da matriz dos coeficientes, pois o determinante de uma matriz cuja linha (ou coluna) seja toda igual a zero, resulta em um determinante igual a zero. Vale lembrar que a classificação de um sistema linear pelo determinante é: “caso o determinante seja zero denominamos este sistema como SPI”.

Quando possuímos um escalonamento completo, podemos analisar o sistema de três formas diferentes, todas elas dependendo da última linha. Dessa forma, quando temos na última linha:

• Uma equação do 1º grau com uma incógnita. (Ex.: 3x=3; 2y=4;…): o sistema será SPD (sistema possível determinado);

• Uma igualdade verdadeira sem incógnitas. (Ex.: 0 = 0; 2 = 2; 4 = 4): o sistema será SPI (Sistema possível indeterminado)

• Uma igualdade falsa sem incógnitas. (Ex.: 1 = 0; 2 = 1; 3 = -3; 5 = 2): o sistema é SI (Sistema impossível).

• Igualdade com impossibilidade de determinação do valor da incógnita. (Ex.: 0.x=10; 0w=5; 0y=2). Veja que as incógnitas estão multiplicadas por zero e igualadas a um valor. Afirmamos que é impossível determinar o valor da incógnita, pois qualquer que seja o seu valor, quando multiplicarmos pelo coeficiente 0 (zero) o resultado será nulo.

Vejamos alguns exemplos:

Exemplo 1:

Trata-se de um sistema 3x3, totalmente escalonado e com uma equação do 1º grau em sua última linha. Portanto, espera-se obter uma solução determinada.

Da 3ª equação temos que z = 2.

Na 2ª equação, substituímos o valor de z. Temos que y = 4.

Substituindo o valor de z e y na primeira equação, teremos que x = 2.

Com isso, então, o sistema é possível e determinado, e seu conjunto-solução é:

S ={(2, 4, 2)}

Exemplo 2:

Sistema 3x3 totalmente escalonado.

Note que na 3ª equação não é possível determinar o valor da incógnita z, ou seja, é um sistema impossível.

Conjunto solução: S = ∅

Exemplo 3:

Sistema 2x3, escalonado. Trata-se de um sistema incompleto, pois a incógnita z não foi esboçada isoladamente. Desse modo, este sistema é um sistema possível indeterminado, pois o sistema possui mais incógnitas do que equações.

Sendo assim, para resolvê-lo procederemos da seguinte maneira: a incógnita que não foi escalonada será uma incógnita livre, ela poderá assumir qualquer valor, portanto daremos a ela um valor qualquer (α).

z = α

Tendo um valor qualquer para a incógnita z, podemos substituir este valor na segunda equação e encontrar um valor para a incógnita y. Note que o valor de y dependerá de cada valor adotado para o valor de z.

2y - 2α = 6; 2y = 6 - 2α; y = 3 – α.

Como conhecemos o valor de z e de y podemos substituí-los na 1ª equação.

x -3 + α + α = 3; x = 2α

Sendo assim, o conjunto solução será dado da seguinte forma:

S = {(2α, 3 – α, α)} (Solução “genérica”, para cada α obtém-se uma solução diferente)

O sistema é indeterminado, pois ele admite infinitas soluções, basta variar o valor de α.

Faça α = 1. S = {(2, 2, 1)}

Faça α = 0. S = {(0, 3, 0)}

Faça α = 3. S = {(6, 0, 3)}

Dizemos que o grau de indeterminação deste sistema é 1, pois o número de incógnitas menos o número de equações é igual a 1 (3-2 = 1); e dizemos também que temos uma variável livre.

Exemplo 4:

Sistema 2x4. Trata-se de um sistema possível e indeterminado. Temos duas equações e quatro incógnitas, nas quais duas delas serão incógnitas livres (y e z). Grau de indeterminação é 2.

Faça z = α e y = β, onde α e β pertencem ao conjunto dos números reais.

Na segunda equação temos: α + t = 1 ⇒ t = 1 – α

Na primeira equação teremos:

x – β + 2α – 3( 1 – α) = 5   ⇒  x = 8 – 5α + β

Logo a solução geral será:

S = {( 8 – 5α + β, β, α, 1 – α )}.