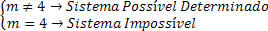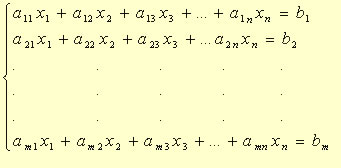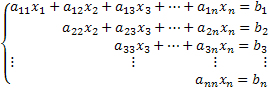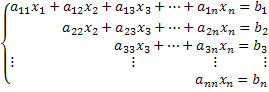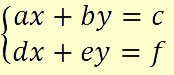Discutir um sistema linear consiste em analisá-lo de forma a determinar os valores dos coeficientes das equações que fazem com que o sistema possa ser Possível e Determinado (SPD), Possível e Indeterminado (SPI) e Impossível (SI). Impondo condições sobre um dos coeficientes já é possível discutir esse sistema e relacionar quais valores esse coeficiente pode assumir, relacionando-os com as classificações dos sistemas, como vimos anteriormente.
Para discutir um sistema serão necessários alguns conceitos importantes: o cálculo do determinante da matriz que possui os coeficientes das equações que constituem o sistema linear, o escalonamento de um sistema linear e a classificação de sistemas lineares escalonados.
Faremos uma análise do determinante dos coeficientes de uma matriz 2x2, entretanto essa análise é válida para qualquer sistema com n equações e n incógnitas.
Considere o seguinte sistema:
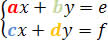
O determinante dos coeficientes é dado pela seguinte matriz-determinante:
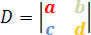
Obteremos as condições para que o sistema linear seja classificado de acordo com esse determinante. Portanto, temos as seguintes condições:

Quando encontramos o valor para os coeficientes que faz com que o determinante seja diferente de zero, estaremos então obtendo um sistema possível e determinado. Assim, basta escolhermos a melhor maneira de solucioná-lo e obter o conjunto solução.
Entretanto, quando encontramos as condições para o determinante ser zero, deveremos continuar a analisar o sistema, substituindo esse valor que resulta em um determinante nulo, a fim de analisarmos o sistema e determinarmos se ele será SPI (Sistema Possível Indeterminado) ou SI (Sistema Impossível).
Veja alguns exemplos para compreender melhor essas situações descritas.
Discuta o sistema, analisando os valores do coeficiente k:
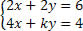
Devemos calcular o determinante D:
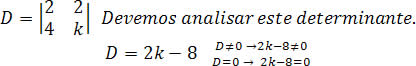
Façamos a análise para do coeficiente k, para que o sistema seja SPD.
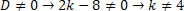
Com isso, podemos concluir que para calcular o valor de k que seja diferente de 4, teremos um sistema SPD.
Em contrapartida, devemos analisar o valor que gera um sistema SPI ou SI. Para determinar essa classificação, devemos substituir o valor obtido e analisar o sistema.
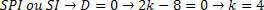
Substituindo no sistema, teremos:
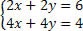
Divida a segunda equação por 2 e analise o sistema:
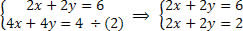
Note que temos equações iguais, porém dando resultados diferentes, ou seja, equações incoerentes, incompatíveis, resultando, assim, em um sistema SI.
Por fim, analisando o sistema de acordo com o coeficiente k, temos: