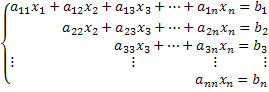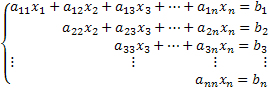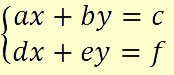Processo para escalonar um sistema linear

Bem, sabemos que nem todos os sistemas lineares serão escritos, previamente, de forma escalonada. Portanto, precisamos encontrar uma forma de obter um sistema equivalente, que seja um sistema escalonado.

Vale ressaltar que dois sistemas são ditos equivalentes quando estes possuem o mesmo conjunto solução.

O processo de escalonamento de um sistema linear ocorre por meio de operações elementares, que são iguais às utilizadas no teorema de Jacobi.

Portanto, para escalonarmos um sistema, podemos seguir um roteiro com alguns procedimentos. Utilizaremos um sistema linear para explicitarmos tais passos.

• As equações podem ser trocadas de posição e ainda assim teremos um sistema equivalente.

Para facilitar o procedimento, aconselhamos que a primeira equação seja aquela sem coeficientes nulos e que o coeficiente da primeira incógnita seja, de preferência, igual a 1 ou –1. Esta escolha facilitará os passos seguintes.

• Podemos multiplicar todos os termos de uma equação pelo mesmo número real diferente de zero:

Este é um passo que pode ser utilizado dependendo do sistema a ser trabalhado, pois ao realizar este procedimento você estará escrevendo a mesma equação, entretanto com coeficientes diferentes.

Na verdade este é um passo complementar ao próximo.

• Multiplique todos os membros de uma equação por um mesmo número real, que seja diferente de zero, e some esta equação obtida à outra equação do sistema.

Com isso, substituiremos esta equação obtida no lugar da segunda equação. Note que esta equação já não possui uma das incógnitas.

Repita este processo para as equações que possuem mesma quantidade de incógnitas, no nosso exemplo seriam as equações 2 e 3.

Note que a 1ª equação continuou normal, mesmo após ter sido multiplicada por -2. Esta multiplicação é feita para obtermos coeficientes opostos (sinais trocados) para que quando a soma seja realizada o coeficiente se anule e o escalonamento seja feito. Não existe a necessidade de escrever a primeira equação de maneira diferente, mesmo se você multiplicá-la.

• Uma possibilidade que existe neste processo é a obtenção de uma equação com todos os coeficientes nulos, entretanto com o termo independente diferente de zero. Caso isso aconteça, podemos afirmar que o sistema é impossível, ou seja, não existe solução que o satisfaça.

Exemplo: 0x + 0y = 1

Vejamos um exemplo de sistema a ser escalonado.

Note que a incógnita faltando na ultima equação é a y, ou seja, a partir das duas primeiras devemos obter uma equação que tenha apenas as incógnitas x e z, em outras palavras, devemos escalonar a incógnita y.

Sendo assim, teremos um sistema equivalente.

Ao somar a segunda e a terceira equação, teremos o seguinte sistema:

Com isso, obtemos um sistema escalonado.