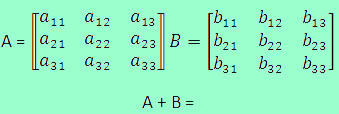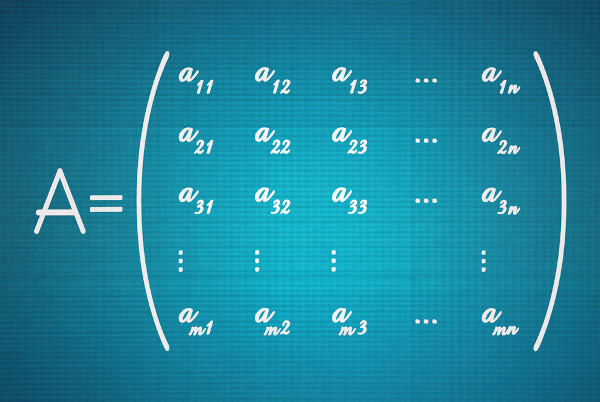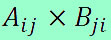O teorema de Laplace consiste num método de calcular o determinante de matrizes quadradas de ordem n ≥ 2 utilizando o cofator.
Lembrando que o cofator do elemento aij de uma matriz quadrada é o número:
![]()
Para calcular o determinante de uma matriz M quadrada de ordem n ≥ 2 utilizando o Teorema de Laplace, devemos proceder da seguinte forma:
1. Escolha qualquer fila (linha ou coluna) da matriz M.
2. Multiplique cada elemento da fila pelo seu respectivo cofator.
3. O teorema de Laplace diz que o determinante da matriz M será a soma dos produtos dos elementos da fila pelos seus respectivos cofatores.
Como já dispomos de métodos práticos para o cálculo do determinante de matrizes quadradas de ordem 2 e 3, é interessante aplicar o Teorema de Laplace para matrizes de ordem maior ou igual a 4.
Faremos alguns exemplos de aplicação do teorema proposto.
Exemplo 1. Calcule o determinante da matriz abaixo utilizando o dispositivo prático de Sarrus e o Teorema de Laplace.
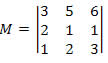
Solução: Primeiro, vamos calcular o determinante utilizando o método prático de Sarrus.
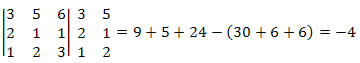
Agora, vamos calcular o determinante utilizando o Teorema de Laplace.
Devemos escolher qualquer linha ou coluna da matriz M. Nesse caso, escolheremos a linha 2.
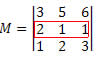
Agora, multiplicaremos cada elemento da linha pelo seu respectivo cofator:
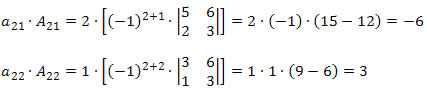
![]()
Logo, o determinante será a soma desses produtos, ou seja:
D = – 6 + 3 +( – 1) = – 4.
Observe que nesse caso o dispositivo prático de Sarrus torna o cálculo do determinante bem mais simples que o Teorema de Laplace, como foi dito anteriormente.
Exemplo 2. Calcule o determinante da matriz a seguir utilizando o Teorema de Laplace.
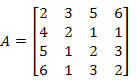
Solução: Devemos escolher uma linha ou uma coluna da matriz A.
Se escolhermos a coluna 2, teremos:

Pelo teorema de Laplace, sabemos que:
D = a12?A12 + a22?A22 + a32?A32 + a42?A42
Segue que:
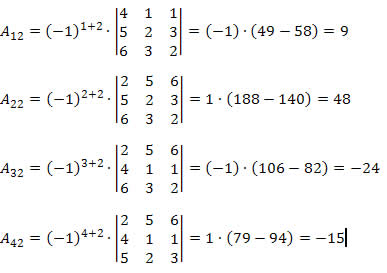
Assim, o determinante da matriz A será:
D = 3?9 + 2?48 + 1?(-24) + 1?(-15) = 27 + 96 - 24 - 15 = 84
Videoaulas relacionadas: