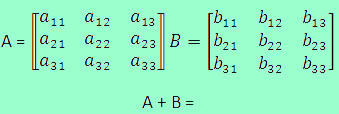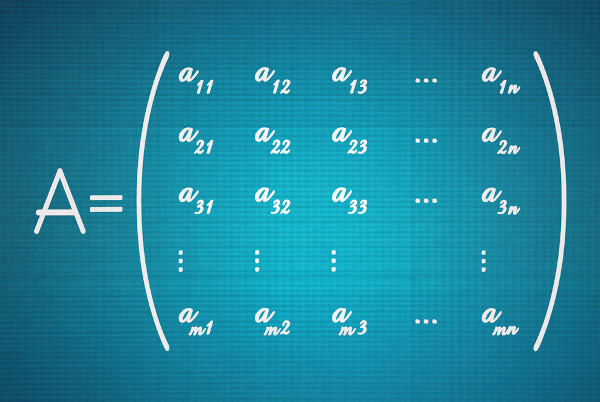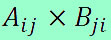Igualdade de matrizes

O estudo de matrizes e determinantes está relacionado à resolução de sistemas lineares e ao cálculo da área de um triângulo no plano cartesiano. Dadas duas matrizes A e M, podemos afirmar que elas são iguais se:

1. Elas apresentarem a mesma ordem.
2. Todos os elementos de A forem iguais aos correspondentes de M.

Por exemplo, dada uma matriz A_{2 x 2}, ela será igual à matriz B se B tiver ordem 2 x 2 e se a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁ e a₂₂ = b₂₂.

Abaixo segue o exemplo de duas matrizes iguais.

Observe que elas apresentam a mesma ordem, 2 x 2, e os elementos correspondentes são iguais.

Vejamos alguns exemplos de exercícios envolvendo igualdade entre matrizes.

Exemplo 1. Determine o valor de x e y para que se tenha A = B, sendo:

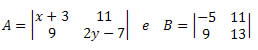
Solução: Observe que as duas matrizes já possuem a mesma ordem, 2 x 2. Logo, temos que:

Para que a matriz A seja igual à matriz B, deveremos ter as seguintes igualdades:

Portanto, x = – 8 e y = 10.

Exemplo 2. Quais os possíveis valores de x, y, z e w para que ocorra A = B, sendo:

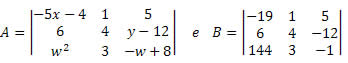
Solução: As matrizes A e B apresentam a mesma ordem, 3 x 3. Assim, teremos:

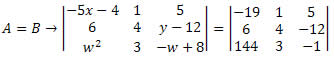
Daí, obtemos as seguintes igualdades:

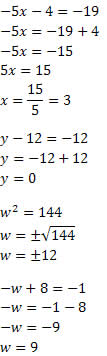
Videoaulas relacionadas: