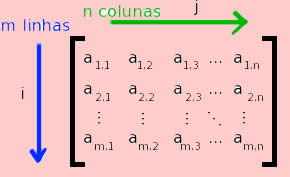
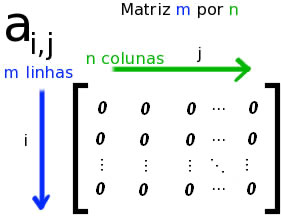
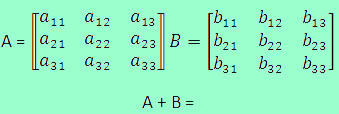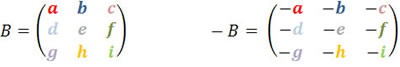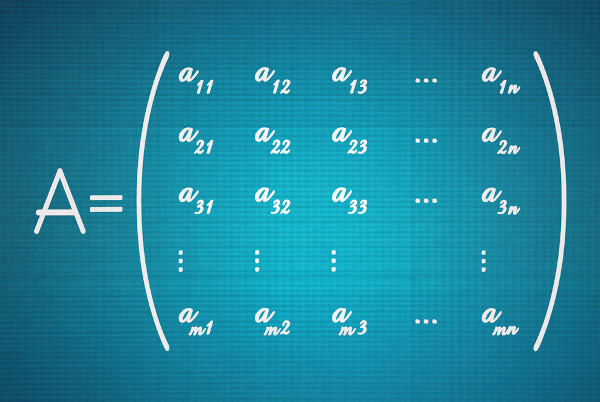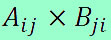O estudo das matrizes deve ser considerado de grande importância, constituindo numa importante ferramenta da Matemática presente em áreas relacionadas aos cálculos, como a Engenharia, a Informática e outras. Nos estudos estatísticos, as matrizes constituem tabelas que objetivam por organizar os dados distribuídos por linhas e colunas.
Assim como os números, as matrizes possuem propriedades operatórias, podem ser adicionadas. Considerando duas matrizes A e B de mesma ordem, isto é, mesmo número de linhas e colunas, a soma entre elas constituirá em uma matriz C de mesma ordem das adicionadas. Os termos deverão ser somados de acordo com suas posições. Por exemplo, se somarmos duas matrizes de ordem 3x3, as adições dos elementos respeitarão a seguinte situação:
a11 + b11 = c11
a12 + b12 = c12
a13 + b13 = c13
a21 + b21 = c21
a22 + b22 = c22
a23 + b23 = c23
a31 + b31 = c32
a32 + b32 = c32
a33 + b33 = c33
Observe:
Exemplo 1
Adicionar as matrizes A e B.
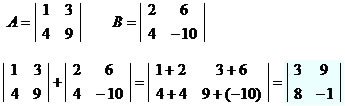
A + B = C ↔ aij + bij = cij
A matriz se enquadra nas propriedades da adição, dada a matriz A, B, C e O, sendo O nula, vale as propriedades da:
Comutação: A + B = B + A
Associação: A + (B + C) = (A + B) + C
Elemento neutro: A + O = O + A = 0
Videoaula relacionada: