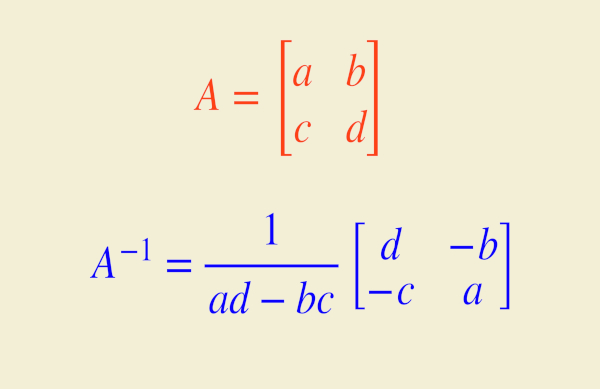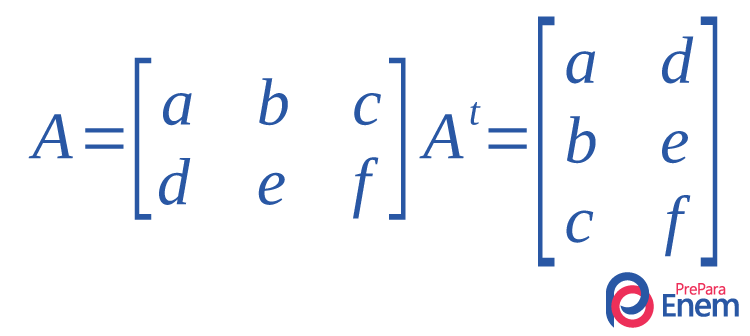Matriz inversa é o elemento neutro da multiplicação entre matrizes. Chamamos de matriz inversa da matriz A a matriz A-1, em que, ao multiplicarmos a matriz A pela matriz A-1, temos como produto a matriz identidade In, logo, sabemos que A ⋅ A-1 = In. Para encontrar a inversa de uma matriz com elementos conhecidos, utilizamos a igualdade do produto entre as matrizes, resolvendo uma equação para determinar os elementos da inversa. No estudo das matrizes inversas, há algumas propriedades importantes: uma matriz quadrada tem matriz inversa se, e somente se, seu determinante for diferente de zero.
Leia também: Matrizes — o que são, elementos tipos e representações
Tópicos deste artigo
- 1 - Resumo sobre matriz inversa
- 2 - Videoaula sobre matriz inversa
- 3 - O que é matriz inversa?
- 4 - Como calcular a matriz inversa
- 5 - Determinante da matriz inversa
- 6 - Propriedades da matriz inversa
- 7 - Exercícios resolvidos sobre matriz inversa
Resumo sobre matriz inversa
- A matriz inversa de A, denotada por A-1, satisfaz a condição A × A-1 = I, em que I é a matriz identidade.
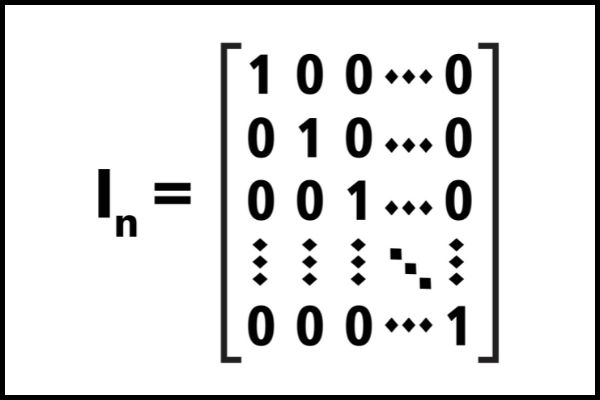
- A matriz identidade é a matriz que tem os elementos da diagonal principal iguais a 1 e os demais elementos iguais a zero.
- A matriz tem inversa se ela for quadrada e ter determinante diferente de zero.
- Existem propriedades específicas de matrizes inversas.
Videoaula sobre matriz inversa
O que é matriz inversa?
Dada a matriz A, a matriz inversa da matriz A, denotada por A-1, é a matriz cujo produto da matriz A por ela seja igual à matriz identidade, ou seja:
\(A \cdot A^{-1} = I_n \)
A matriz identidade é a matriz cujos termos da diagonal principal são iguais a 1 e os demais termos são iguais a zero.
Exemplos de matriz identidade:
\(I_2 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \\\)
\(I_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \\\)
\(I_4 = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\)
Exemplo de matriz inversa:
Dada a matriz \(A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \), a matriz inversa de A é a matriz \(A^{-1} = \begin{pmatrix} -2 & 1 \\ \frac{3}{2} & \frac{-1}{2} \end{pmatrix} \), pois temos que:
\(\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} -2 & 1 \\ \frac{3}{2} & \frac{-1}{2} \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \)
Como calcular a matriz inversa
Para calcular a matriz inversa, existem diferentes métodos, faremos o mais clássico deles, que é a resolução de equações envolvendo matrizes. Vejamos como resolvê-lo no exemplo a seguir.
Exemplo:
Calcule a matriz inversa da matriz:
\(A = \begin{pmatrix} 4 & 4 \\ 8 & 6 \end{pmatrix} \)
Para encontrar a matriz inversa de A, vamos representar o seguinte produto:
\(\begin{pmatrix} 4 & 4 \\ 8 & 6 \end{pmatrix} \cdot \begin{pmatrix} a & b \\ c & d \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \)
Agora, vamos realizar a multiplicação entre essas matrizes e encontrar as equações:
\(\text{I} \quad 4a + 4c = 1 \ \quad \text{II} \quad 4b + 4d = 0 \ \quad \text{III} \quad 8a + 6c = 0 \ \quad \text{IV} \quad 8b + 6d = 1 \)
Da equação II, temos que:
\(4b+4d=0\)
\(4b=-4d\)
\(b=-d\)
Substituindo na equação IV, temos que:
\(8b+6d=1\)
\(8(-d) + 6d = 1 \)
\(-8d+6d=1\)
\(-2d=1\)
\(d = \frac{1}{-2} = \frac{-1}{2} \)
Então, sabemos que b = - d.
Logo, temos que:
\(b = -\left( \frac{-1}{2} \right) = \frac{1}{2} \)
Da equação III, temos que:
\(8a+6c=0\)
\(8a=6c\)
\(a = \frac{-6c}{8} \)
\(a = \frac{-3c}{4} \)
Substituindo em I, temos que:
\(4a+4c=1\)
\(4 \cdot \left( \frac{-3c}{4} \right) + 4c = 1 \)
\(-3c+4c=1\)
\(c=1\)
Então, temos que:
\(a = \frac{-3c}{4} \)
\(a = \frac{-3 \cdot 1}{4} \)
\(a = \frac{-3}{4} \)
Sendo assim, a matriz inversa será:
\(A^{-1} = \begin{pmatrix} \frac{-3}{4} & \frac{1}{2} \\ 1 & \frac{-1}{2} \end{pmatrix} \)
Esse método pode se estender para matrizes de qualquer ordem, entretanto, quanto maior for a ordem, mais equações teremos.
Veja também: O que é uma matriz nula?
Determinante da matriz inversa
Existe um método específico para matrizes de ordem 2. Caso a matriz seja de ordem 2, podemos calculá-la assim:
Dada a matriz \(A = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \)
\(A^{-1} = \frac{1}{\det(A)} \cdot \begin{pmatrix} d & -b \\ -c & a \end{pmatrix} \)
Exemplo:
Dada a matriz:
\(A = \begin{pmatrix} 2 & 1 \\ 2 & -2 \end{pmatrix} \)
De modo geral, sabemos que a matriz A tem matriz inversa se, e somente se, det(A) ≠ 0.
Propriedades da matriz inversa
A matriz inversa tem propriedades importantes:
- A inversa da matriz inversa A é igual à matriz A: (A-1)-1 = A.
- Uma matriz só tem inversa se o seu determinante for diferente de zero.
- Caso o determinante det(A) seja igual a zero, a matriz não tem matriz inversa.
- A matriz transposta da matriz inversa é igual à matriz inversa da matriz transposta
(A-1)t = (At)-1.
- A inversa de uma matriz identidade é sempre igual a ela mesma: I-1 = I.
- A inversa do produto de duas matrizes é igual ao produto das inversas: (A×B)-1 = A-1 × B-1.
Saiba mais: Quais são as propriedades de uma matriz transposta?
Exercícios resolvidos sobre matriz inversa
Questão 1
A matriz \(A = \begin{pmatrix} 5 & 4 \\ c & 2 \end{pmatrix} \) é uma matriz que não tem matriz inversa. Sendo assim, o valor de c é:
a) 2/3
b) 2/5
c) 5/2
d) 3/2
e) 10/2
Resolução:
Alternativa C
A matriz não admite inversa se o seu determinante for igual a zero, sendo assim, basta calcular o terminante da matriz A igualando-o a zero:
\(\det(A) = 5 \cdot 2 - 4c = 0 \)
\(10-4c=0\)
\(-4c=-10\)
\(4c=10\)
\(c = \frac{10}{4} \)
\(c = \frac{5}{2} \)
Questão 2
Seja \(A = \begin{pmatrix} 2 & 5 \\ 3 & 7 \end{pmatrix} \), qual é a matriz inversa de A?
a) \(\begin{pmatrix} -7 & 5 \\ 3 & -2 \end{pmatrix} \)
b) \(\begin{pmatrix} -7 & 5 \\ -3 & -2 \end{pmatrix} \)
c) \(\begin{pmatrix} -7 & -5 \\ -3 & -2 \end{pmatrix} \)
d) \(\begin{pmatrix} 7 & -5 \\ -3 & 2 \end{pmatrix} \)
e) \(\begin{pmatrix} 7 & 5 \\ 3 & -2 \end{pmatrix} \)
Resolução:
Alternativa A
Primeiro calcularemos o determinante de A.
\(\det(A) = 2 \cdot 7 - 5 \cdot 3 = 14 - 15 = -1 \)
Agora, aplicando na fórmula:
\(A^{-1} = \frac{1}{\det(A)} \cdot \begin{pmatrix} d & -b \\ -c & a \end{pmatrix} \)
\(A^{-1} = \frac{1}{-1} \cdot \begin{pmatrix} 7 & -5 \\ -3 & 2 \end{pmatrix} \)
\(A^{-1} = -1 \cdot \begin{pmatrix} 7 & -5 \\ -3 & 2 \end{pmatrix} \)
\(A^{-1} = \begin{pmatrix} -7 & 5 \\ 3 & -2 \end{pmatrix} \)
Fonte
Boldrini, José Luiz et al. Álgebra Linear. 3ª ed. Harbra, 1986.