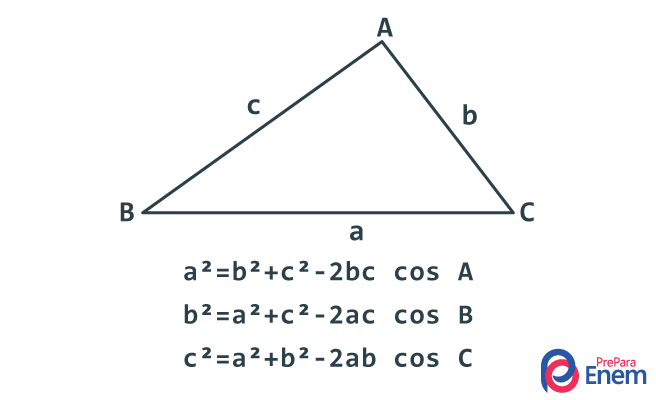
Também conhecida como teorema dos cossenos, a lei dos cossenos demonstra uma relação entre a medidas dos lados de um triângulo e um ângulo. Para encontrar a medida de um dos lados de um triângulo, conhecendo a medida do ângulo oposto a esse e dos outros dois lados, recorremos à lei dos cossenos.
A fórmula da lei dos cossenos para encontrar a medida do lado a é a² = b² + c² – 2 · b · c · cosA. Logo, a lei dos cossenos determina que o quadrado de um dos lados do triângulo é igual à soma dos quadrados dos outros dois lados, menos o dobro do produto de ambos pelo cosseno do ângulo formado entre eles. A principal aplicação da lei dos cossenos é encontrar medidas desconhecidas em um triângulo. Note que, nesse caso, o triângulo não precisa ser retângulo, como nas razões trigonométricas e no teorema de Pitágoras.
Tópicos deste artigo
- 1 - Resumo sobre a lei dos cossenos
- 2 - Videoaula sobre a lei dos cossenos
- 3 - Fórmula da lei dos cossenos
- 4 - Demonstração da lei dos cossenos
- 5 - Aplicação da lei dos cossenos
- 6 - Exercícios resolvidos sobre lei dos cossenos
Resumo sobre a lei dos cossenos
-
A lei dos cossenos é conhecida também como teorema dos cossenos.
-
Utilizamos a lei dos cossenos para encontrar lados desconhecidos de um triângulo.
-
Dado um triângulo ABC, a lei dos cossenos determina que:
a² = b² + c² – 2b · c · cosA
b² = a² + c² – 2a · c · cosB
c² = a² + b² – 2a · b · cosC
Videoaula sobre a lei dos cossenos
Fórmula da lei dos cossenos
Conhecemos como lei dos cossenos, ou teorema dos cossenos, uma relação entre os lados e ângulos de um triângulo. A lei dos cossenos mostra que o quadrado de um dos lados do triângulo é igual à soma dos quadrados dos outros dois lados, menos o dobro do produto de ambos pelo cosseno do ângulo formado entre eles.
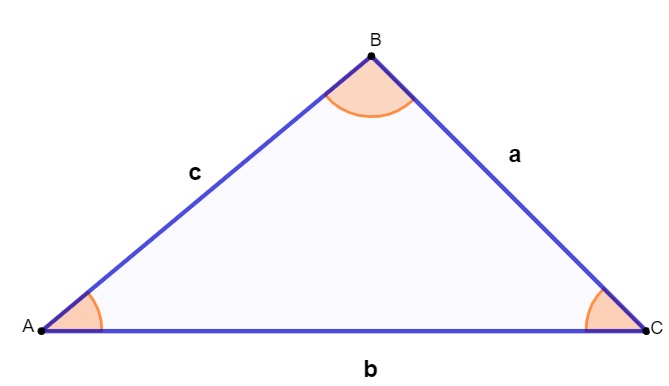
As fórmulas da lei dos cossenos são:
|
a² = b² + c² – 2b · c · cosA b² = a² + c² – 2a · c · cosB c² = a² + b² – 2a · b · cosC |
Demonstração da lei dos cossenos
Para demonstrar a lei dos cossenos, primeiramente construiremos um triângulo de lados ABC. Opostos aos ângulos A, B e C, os lados terão medidas a, b e c, respectivamente. O segmento DC mede a – m, como na imagem a seguir.
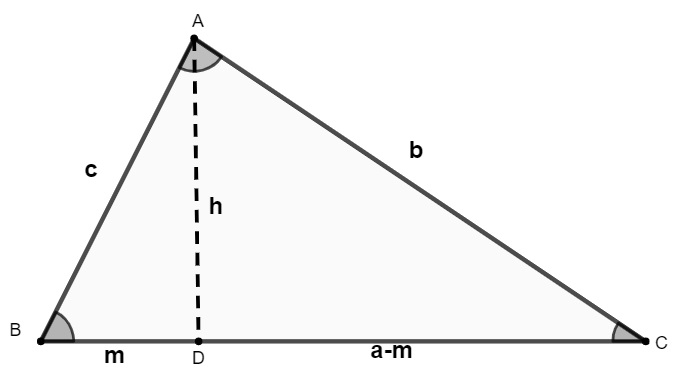
De início, analisando o triângulo ABD, constatamos que:
cosB = m/c
c · cosB = m
Agora, aplicamos o teorema de Pitágoras, obtendo:
c² = m² + h²
Podemos reescrever isso como:
h² = c² – m²
Aplicando o teorema de Pitágoras no triângulo ACD:
b² = h² + (a – m)²
b² = h² + a² – 2am + m²
Sabemos que h² = c² – m², então substituindo h² por c² – m², obtemos:
b² = c² – m² + a² – 2am + m²
b² = c² + a² – 2am
Sabemos também que m = c · cosB, então:
b² = c² + a² – 2a · c · cosB
Fica demonstrada, assim, a lei dos cossenos. Para as demais relações, a forma de demonstração é a mesma.
Veja também: Lei dos senos — estabelece identidades trigonométricas para um triângulo qualquer
Aplicação da lei dos cossenos
Vejamos a seguir uma aplicação da lei dos cossenos para encontrar a medida do lado x no triângulo a seguir.
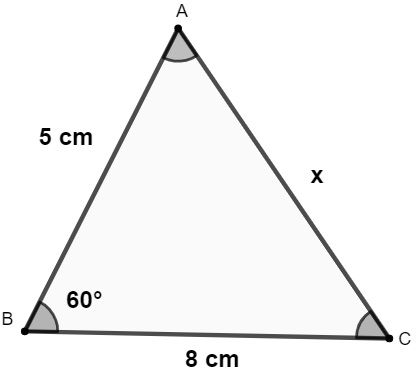
Aplicando a lei dos cossenos, temos:
x² = 5² + 8² – 2 · 5 · 8 · cos60°
x² = 25 + 64 – 80 · cos60°
Consultando o valor do cos60°, descobrimos ele equivale a 1/2. Dessa forma, calculamos o seguinte:
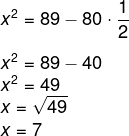
Portanto, a medida de x é 7 cm.
Saiba mais: Cosseno da soma e diferença de dois arcos — auxilia o cálculo de funções circulares
Exercícios resolvidos sobre lei dos cossenos
Questão 1
(Funiversa) Investigações de um crime com arma de fogo indicam que um atirador atingiu diretamente dois pontos, B e C, a partir de um único ponto A. São conhecidas as distâncias: AC = 3 m, AB = 2 m e BC = 2,65 m. A medida do ângulo formado pelas duas direções nas quais o atirador disparou os tiros é mais próxima de:
A) 30°
B) 45°
C) 60°
D) 75°
E) 90°
Resolução:
Alternativa C
Sendo A o ângulo que queremos descobrir, temos:
a² = b² + c² – 2 · b · c · cosA
2,65² = 3² + 2² – 2 · 3 · 2 · cosA
7,0225 = 9 + 4 – 12 · cosA
Como queremos o valor aproximado, arredondamos 7,0225 para 7:
7 = 9 + 4 – 12 · cosA
7 = 13 – 12 · cosA
7 – 13 = – 12 · cosA
– 6 = – 12 · cosA
– 6 : ( – 12) = cosA
0,5 = cosA
O ângulo que possui cosseno igual a 0,5 é o ângulo de 60°.
Questão 2
(Enem 2017) Uma desenhista projetista deverá desenhar uma tampa de panela em forma circular. Para realizar esse desenho, ela dispõe, no momento, de apenas um compasso, cujo comprimento das hastes é de 10 cm, um transferidor e uma folha de papel com um plano cartesiano. Para esboçar o desenho dessa tampa, ela afastou as hastes do compasso de forma que o ângulo formado por elas fosse de 120°. A ponta seca está representada pelo ponto C, a ponta do grafite está representada pelo ponto B e a cabeça do compasso está representada pelo ponto A conforme a figura.
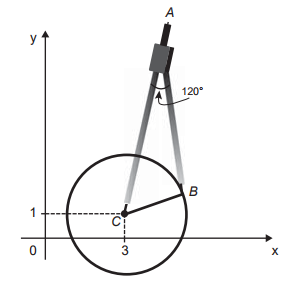
Após concluir o desenho, ela o encaminha para o setor de produção. Ao receber o desenho com a indicação do raio da tampa, verificará em qual intervalo este se encontra e decidirá o tipo de material a ser utilizado na sua fabricação, de acordo com os dados.
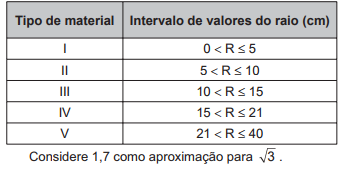
O tipo de material a ser utilizado pelo setor de produção será
A) I.
B) II.
C) III.
D) IV.
E) V.
Resolução:
Alternativa D
O compasso forma com o raio da circunferência um triângulo com um ângulo de 120°, um lado oposto a esse ângulo igual ao raio R da circunferência e os outros dois lados com 10 cm cada. Então, aplicando a lei dos cossenos:
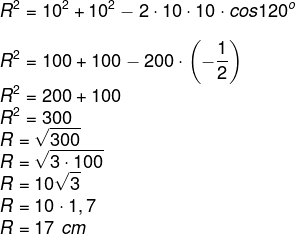
Como 17 está entre 15 e 21, será escolhido o material IV.