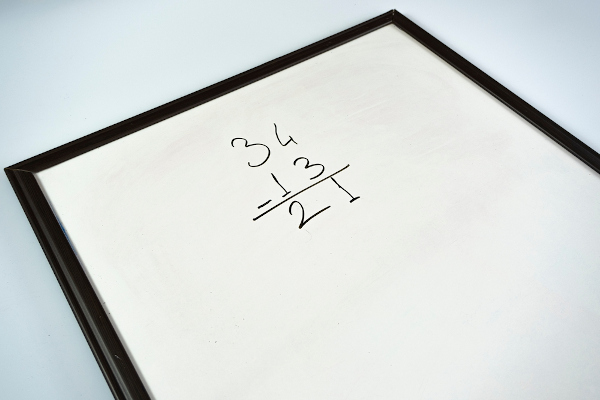A divisão é uma das quatro operações matemáticas básicas. Ela é essencial para a compreensão do raciocínio matemático, sendo base para vários conceitos da área. Essa operação reparte uma quantidade em partes iguais de acordo com a operação proposta.
É importante compreender que cada elemento da divisão tem um nome e que utilizamos um algoritmo para facilitar os cálculos. Nesse algoritmo, os elementos são conhecidos como dividendo, divisor, quociente e resto, sendo cada um deles de extrema importância para se compreender essa operação.
Leia também: Quais são as regras de divisibilidade?
Tópicos deste artigo
- 1 - O que é a divisão?
- 2 - Elementos da divisão
- 3 - Divisão passo a passo
- 4 - Divisão de números com vírgula
- 5 - Jogo de sinal da divisão
- 6 - Propriedades da divisão
- 7 - Exercícios resolvidos
O que é a divisão?

A divisão é a operação contrária da multiplicação, então, para compreendê-la, é fundamental o domínio da multiplicação.
Exemplo:
10 : 2 → Ao escrever essa operação, estamos, na realidade, buscando saber quantas vezes o número 2 cabe no número 10. Isso significa buscar qual deve ser o número que, multiplicado por 2, gera o resultado 10. Tendo domínio da tabuada, é fácil lembrar que 2 · 5 = 10. Assim, podemos afirmar que:
10 : 2 = 5, pois 2·5 = 10
Com esse mesmo raciocínio, podemos resolver outros exemplos.
24 : 6 = 4, pois 4 · 6 = 24
Existem casos em que a divisão não é exata, por exemplo:
31: 5
Essa não é uma divisão exata, pois sabemos que 5 · 6 = 30, que é o valor multiplicado por 5 que chega mais próximo de 31. Então, dizemos que o resultado é 6, e o resto é 1.
Elementos da divisão
Em uma divisão, existem elementos importantes, a saber:
-
o número N a ser dividido é conhecido como dividendo;
-
o número d que irá dividi-lo é conhecido como divisor;
-
o resultado q da divisão é chamado de quociente;
-
e o que restar na divisão, representado por r, recebe o nome de resto.
Para ficar claro o que é cada um desses elementos, utilizamos o chamado método de chaves, que é um algoritmo, ou seja, um conjunto de técnicas, utilizado para calcular a divisão entre números maiores, isto é, aqueles que estão além dos que conhecemos na tabuada.
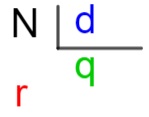
N → dividendo
d → divisor
q → quociente
r → resto
Exemplo:
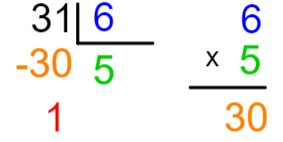
Nesse caso, os elementos são:
-
dividendo: 31
-
divisor: 6
-
quociente: 5
-
resto: 1
Veja também: Dicas para o cálculo da multiplicação
Divisão passo a passo
Para realizar a divisão, é necessário dominar o algoritmo. Existem algoritmos diferentes para calcular a divisão, mas o mais comum é o método de chaves. Esse método tem como objetivo facilitar a realização do cálculo e, para isso, seguimos alguns passos.
Exemplo:
125 : 5
1º passo: montar o algoritmo com o dividendo e o divisor em seus devidos lugares.
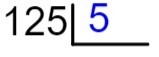
2º passo: analisar o primeiro número do dividendo, começando sempre da esquerda para a direita. No caso o 1, é possível dividi-lo por 5? Se for, realizaremos a divisão. Como 1 é menor que 5, não é possível; então, vamos selecionar os dois primeiros números — no caso o 12. Como 12 é maior do que 5, é possível dividir.

3º passo: procurar qual número que, ao multiplicá-lo por 5, é igual ou chega próximo de 12, não podendo nunca ser maior que 12.
Ao recorrer à tabuada do 5, sabemos que 5 x 2 = 10 e que 5 x 3 é maior do que 12. Sendo assim, escrevemos no quociente o número 2.
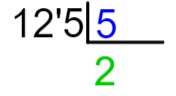
4º passo: ciente de que 2 x 5 = 10, colocaremos o resultado dessa multiplicação abaixo da parte escolhida do dividendo, ou seja, abaixo do 12, e realizaremos a subtração 12 – 10.
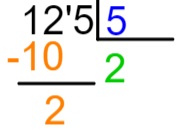
5º passo: após realizar a subtração, vamos colocar, à direita do resultado, o próximo número do dividendo e repetir o processo de divisão.
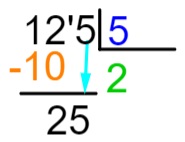
6º passo: agora vamos repetir o processo que fizemos no passo 2, ou seja, qual número que, ao multiplicá-lo por 5, chega mais próximo ou é exatamente igual a 25. Sabemos que 5 x 5 = 25, então acrescentaremos o 5 no quociente e realizaremos a subtração do dividendo pelo resultado da multiplicação.
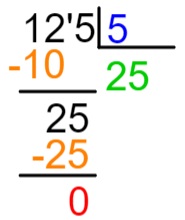
Perceba que não há mais nenhum elemento no dividendo para descer, logo encontramos o resto da divisão.
125 : 5 = 25
Quando o resto é igual a zero, essa divisão é exata; quando o resto não é zero, ela não é exata. Sabemos que a divisão terminou quando não há mais nenhum número para descer do dividendo. Caso seja o interesse, quando o resto é diferente de 0, é possível continuar a divisão trabalhando com uma divisão não exata.
Divisão de números com vírgula
Realizar divisões que resultam em números decimais é bastante comum e também há casos em que o divisor e o dividendo são números decimais. Vamos analisar cada um desses casos.
-
Divisão não exata
A divisão não exata tem como resultado um quociente decimal. Para resolvê-la, realizamos um processo inicialmente parecido com o apresentado anteriormente.
Exemplo:
93 : 2
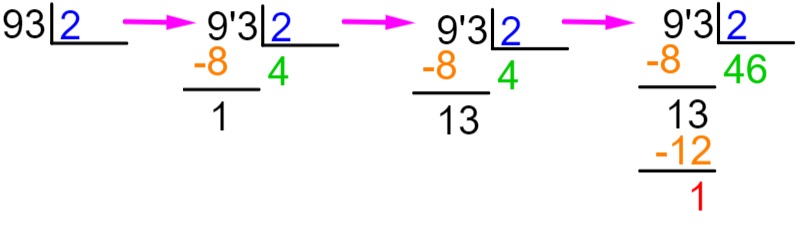
Encontramos um resto igual a 1. Em muitos problemas, o interesse é encontrar o resto da divisão, mas, aqui, o nosso interesse é encontrar o valor da divisão. Nesse caso, acrescentamos uma vírgula no consciente e um zero à direita do resto.
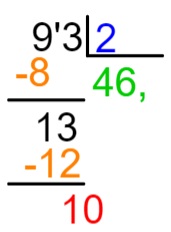
Agora é possível continuar a divisão, procurando qual número que, ao multiplicá-lo por 2, é igual a 10 (nesse caso, o 5).
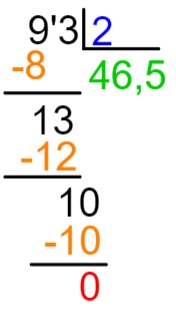
Como o resto foi igual a zero, terminamos a divisão, logo 93 : 2 = 46,5.
Saiba mais sobre esse tipo de divisão lendo o nosso texto: Divisão com resultado decimal.
-
Divisão entre números decimais
Ocorre uma divisão com número decimal quando o divisor ou o dividendo é um número decimal, ou seja, um número que tem vírgula. Antes de realizar a divisão, igualamos o número de casas decimais dos números, colocando zeros ao final. Assim que as casas decimais estiverem igualadas, poderemos retirar a vírgula e realizar a divisão normalmente.
Exemplo:
1,2 : 0,06
Note que, no dividendo, há dois números após a vírgula e, no divisor, apenas um, então vamos igualar as casas depois da vírgula colocando um zero ao final do dividendo.
1,20 : 0,06
Com a quantidade de casas após a vírgula igualada, faremos a divisão:
120 : 006
Como zero à esquerda, nesse caso, não tem valor, faremos a divisão de 120 por 6.
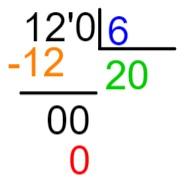
Jogo de sinal da divisão
O jogo de sinal da divisão é igual ao da multiplicação. Então, ao resolver uma divisão entre dois números, basta lembrar que a divisão de dois números com mesmo sinais gera um quociente positivo e que a divisão de dois números com sinais contrários gera um quociente negativo. Para auxiliar, existe uma tabela dos jogos de sinais:
|
Dividendo |
Divisor |
Resultado (quociente) |
|
+ |
+ |
+ |
|
- |
- |
+ |
|
+ |
- |
- |
|
- |
+ |
- |
Observação: Vale ressaltar que essa tabela é exclusiva da multiplicação e da divisão, não se aplicando à adição e à subtração.
Exemplos:
a) -20 : 5 = - 4
b) – 9 : ( -3) = +3
c) 20 : 4 = 5
e) 10 : (-5) = 2
Propriedades da divisão
As propriedades que são válidas para a multiplicação, em sua maioria, não são válidas para a divisão.
-
Divisão não é comutativa
Analisando se a divisão é comutativa, podemos verificar que não, pois a ordem em que a operação é feita é importante, ou seja:
a : b ≠ b : a
É fácil verificar isso, pois 10 : 2 não é a mesma coisa que 2 : 10.
-
A divisão não é associativa
A propriedade associativa diz , ao dividir a : b : c, desconsiderando a ordem, o resultado é o mesmo, ou seja, (a : b) : c teria que ser o mesmo que a : (b : c), o que não ocorre na divisão.
Exemplo:
( 12: 6 ): 2 = 2 : 2 = 1
12 : (6 : 2)= 12: 3 = 4
Note que os resultados são diferentes, logo a divisão não é associativa.
-
Existência de um elemento neutro
Na divisão existe um elemento neutro, que é o número 1. Ao realizar a divisão, sabemos que todo número dividido por 1 é ele mesmo.
Exemplo:
4 : 1 = 4
Acesse também: Quais são as propriedades da multiplicação?
Exercícios resolvidos
Questão 1 – Raíssa trabalha com a venda de chocolates artesanais. Durante a Páscoa, com a alta demanda, ela decidiu se juntar a outras duas amigas e dividir tanto a produção quanto os ganhos de forma igual. Sabendo que havia um total de 372 pedidos, a quantidade de ovos produzidos por cada uma delas foi:
A) 120
B) 124
C) 126
D) 130
E) 134
Resolução
Alternativa B.
Como elas são 3, realizaremos a divisão de 372 por 3.
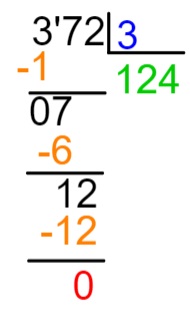
Questão 2 – Analisando a sequência (A,B,C,D,E,A,B,C,D,E…) e sabendo que esse padrão se repete sempre, qual será o termo que ocupa a posição 132 nessa sequência?
A) A
B) B
C) C
D) D
E) E
Resolução
Alternativa B.
Analisando a sequência, é possível perceber que ela se repete a cada 5 números, sendo assim, vamos dividir 132 por 5, para verificar quantas vezes essa sequência se repete. Mas o que nos interessa nesse caso é o resto, pois, a partir dele, é possível verificar onde essa sequência parou e sua última repetição.
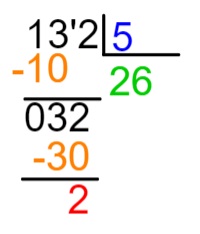
O resultado mostra que a sequência se repetiu 26 vezes e restaram duas letras, ou seja, a segunda letra da sequência será o 132º termo da sequência