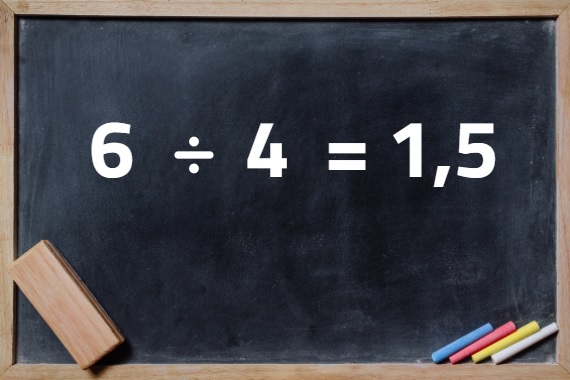Uma divisão possui resultado decimal quando é necessário descobrir a parcela do resto que cabe a cada uma das partes nas quais a quantidade inicial foi dividida. Em outras palavras, quando o resto é diferente de zero e a divisão não é interrompida, o resultado é um número decimal.
Para aprender a encontrar esse tipo de resultado em uma divisão, é preciso ter bons conhecimentos a respeito do algoritmo usado para fazer contas de dividir. Para aprender sobre ele, clique aqui. Além disso, também é importante conhecer algumas das definições básicas da divisão, que serão discutidas adiante.
Veja também: Dicas para o cálculo de multiplicação
Tópicos deste artigo
- 1 - Divisão entre números naturais e primeiro resultado decimal
- 2 - Como encontrar o resultado decimal na divisão?
- 3 - Exemplo:
- 4 - Exemplo 2
Divisão entre números naturais e primeiro resultado decimal
Quando precisamos dividir uma sala de aula que possui 21 alunos em 2 grupos, um aluno sobrará porque ele não pode ser repartido.
Essa divisão pode ser escrita na forma:
21:2 = 10 com resto 1
ou
21 = 2·10 + 1
Essa última é a definição básica da divisão. Nela, 21 é o dividendo, 2 é o divisor, 10 é o quociente ou resultado, e 1 é o resto.
Quando o objeto a ser dividido permite, podemos repartir o resto em partes iguais e distribuir para cada uma das unidades do divisor. No exemplo acima, cada unidade do divisor receberia metade de 1, representada por 0,5, e o resultado final seria 10,5. A divisão não é considerada exata, mas não existe resto.
Veja também: Divisão de polinômios
Como encontrar o resultado decimal na divisão?
Para encontrar o resultado decimal, o primeiro passo é aplicar o algoritmo da divisão para encontrar quociente e resto.
Feito isso e com a certeza de que todos os algarismos do dividendo foram usados e todas as divisões possíveis foram feitas, adicione vírgula logo após o último algarismo do quociente.
Esse passo “nos dá o direito” de adicionar um zero ao final do resto, como se o tivéssemos multiplicado por 10, e prosseguir na divisão.
Existem duas observações muito importantes a serem feitas sobre esse procedimento:
1. Alguns professores ensinam que, no decorrer da divisão, ao dividirmos um número menor do que o divisor, devemos adicionar um zero ao final desse número e outro zero ao final do quociente. Após usar a vírgula, não devemos mais adicionar zeros ao final do quociente por esse motivo. Após o uso da vírgula, podemos adicionar quantos zeros forem necessários ao número a ser dividido;
2. Todo número decimal possui uma única vírgula. Por isso, não podemos adicionar uma segunda vírgula a um número.
Exemplo:
Calcule 35:2
Aplicando o algoritmo da divisão, teremos:
35 | 2
– 2 17
15
– 14
1
35:2 é igual a 17, e o resto é 1. Para prosseguir na divisão, encontrando o resultado decimal, basta adicionar vírgula ao quociente e um zero ao resto:
35 | 2
– 2 17,5
15
– 14
10
– 10
0
Encontrando “resto” zero, a divisão acaba. O resultado da divisão de 35:2 é 17,5.
Exemplo 2
Qual é o resultado da divisão de 100 por 3?
100 | 3
– 9 33,333…
10
– 9
10
– 9
1
Como o resultado é uma dízima periódica, prosseguimos adicionando 3 ao quociente e 0 ao dividendo infinitamente.