A probabilidade é a área da matemática que estuda a chance de determinado evento ocorrer. Presente constantemente no meio científico e no dia a dia, para tomada de decisões, a probabilidade tem várias aplicações importantes em nossas vidas. Devido à importância desse conteúdo, ele é bastante recorrente no Enem, sendo cobrado em todas as provas dos últimos anos.
As questões do Enem exigem um grande cuidado com a interpretação, e, em específico, nas questões que abordam o tema probabilidade, são cobrados outros conteúdos como pré-requisitos, por exemplo:
-
frações
-
razão e proporção
-
números decimais
-
porcentagem
Para se dar bem nas questões de probabilidade, é importante que se tenha uma boa base das definições inicias sobre o tema.
Leia também: Temas de Matemática que mais caem no Enem

Tópicos deste artigo
- 1 - Como probabilidade é cobrada no Enem?
- 2 - O que é probabilidade?
- 3 - Questões sobre probabilidade no Enem
Como probabilidade é cobrada no Enem?
As questões da prova do Enem são elaboradas pensando nas habilidades e competências que o exame espera que o aluno tenha desenvolvido. Essas habilidades e competências podem ser encontradas no documento oficial do Inep conhecido como Matriz Referência do Enem. O conteúdo de probabilidade sempre aparecerá na prova levando-se em consideração essa matriz, já que nela há habilidades específicas voltadas para ele. A probabilidade e a estatística são cobradas em questões envolvidas com a competência de área 7.
-
Competência de área 7 - Compreender o caráter aleatório e não determinístico dos fenômenos naturais e sociais e utilizar instrumentos adequados para medidas, determinação de amostras e cálculos de probabilidade para interpretar informações de variáveis apresentadas em uma distribuição estatística.
Dentro da competência de área 7, há quatro habilidades: H27, H28, H29 e H30. Somente a primeira é específica de estatística, e as habilidades que nos interessam aqui são as seguintes:
-
H28 - Resolver situação-problema que envolva conhecimentos de estatística e probabilidade.
-
H29 - Utilizar conhecimentos de estatística e probabilidade como recurso para a construção de argumentação.
-
H30 - Avaliar propostas de intervenção na realidade utilizando conhecimentos de estatística e probabilidade.
Com o objetivo de cobrar qualquer umas das habilidades anteriores, as questões de probabilidade possuem variações altas em relação à profundidade dos conceitos cobrados nelas. As questões de probabilidade são consideradas, em sua maioria, como fáceis ou médias, sendo rara uma questão difícil, logo, são questões valiosas para o candidato devido à teoria de resposta ao item (TRI).
As questões que envolvem probabilidade exigem quase sempre que o candidato domine as definições básicas do tema. As questões costumam cobrar o cálculo da probabilidade de situações-problemas (podendo ser só a aplicação da fórmula da probabilidade) ou de situações que envolvem probabilidade da união, probabilidade da intersecção ou mesmo probabilidade condicional. No entanto, em questões que envolvem probabilidade condicional, não é necessário o domínio da fórmula de probabilidade condicional, basta analisar-se bem a situação e restringir-se o espaço amostral de acordo com o que se pede na questão.
Então, como preparo, reforce os conceitos básicos da probabilidade e a sua interpretação de problemas. Muitas vezes, mesmo sem que tenhamos visto a fundo os conceitos mais avançados da área, é possível resolver as questões utilizando somente suas noções básicas, o que faz com que o candidato não precise necessariamente decorar uma fórmula para cada um dos casos.
Veja também: Dicas de Matemática para o Enem
O que é probabilidade?
A probabilidade é a área da matemática que realiza o estudo da chance de um determinado evento aleatório ocorrer. Há muitos estudos científicos que usam a probabilidade para conseguir prever comportamentos e modelar situações sociais e econômicas. Os estudos da probabilidade em conjunto com a estatística são amplamente aplicados em eleições ou até mesmo para estudo da contaminação de COVID-19, entre outras situações.
Para se dar bem em probabilidade no Enem, é importante entender bem os conceitos iniciais e a forma de calcular-se a probabilidade. Os conceitos são estes:
-
Experimento aleatório: a probabilidade começa com o objetivo de estudar experimentos aleatórios. Um experimento aleatório é o que, se for realizado sempre nas mesmas condições, terá seu resultado imprevisível, ou seja, é impossível saber qual será seu resultado exato.
-
Espaço amostral: o espaço amostral de um experimento aleatório é o conjunto de todos os resultados possíveis. Ainda que não seja possível prever exatamente o que vai acontecer no experimento, pode-se prever quais são os resultados possíveis. Um exemplo clássico é um lançamento de um dado comum, não é possível saber qual será o resultado, mas existe o conjunto de resultados possíveis, que é o espaço amostral, conhecido também como universo, que, nesse caso, é igual ao conjunto U: {1, 2, 3, 4, 5, 6}.
-
Evento: conhecemos como evento qualquer subconjunto do espaço amostral. De forma mais direta, o evento é o conjunto de resultados que eu pretendo analisar no meu espaço amostral. Por exemplo, no lançamento de um dado, um possível evento é ter um número par como resultado, sendo assim, o conjunto seria A: {2, 4, 6}. Calcular a probabilidade é descobrir a chance de que um evento ocorra.
-
Fórmula da probabilidade: com o interesse em calcular a probabilidade de um determinado evento, dado um experimento aleatório, calculamo-la pela fórmula:
![]()
P(A) → probabilidade do evento A.
n(A) → número de elementos no conjunto A, tratado também como casos favoráveis, ou seja, é a quantidade de resultados favoráveis ao que queremos analisar.
n(U) → número de elementos no conjunto U (universo), tratado também como casos possíveis, ou seja, é a quantidade de resultados possíveis que o experimento aleatório pode ter.
-
Observações importantes sobre probabilidade
O valor da probabilidade pode ser representado por uma fração, um número decimal ou pela forma percentual:
-
A chance de um evento acontecer é sempre um número entre 0 e 100%.
-
Na forma decimal, a probabilidade será sempre entre 0 e 1.
Seja A um evento de probabilidade P(A), a probabilidade de seu evento complementar, ou seja, a chance do evento A não acontecer é calculada por: 1 – P(A), na forma decimal, ou 100% – P(A), na forma percentual.
Dados dois eventos, A e B, como eventos independentes, ou seja, o resultado de um deles não influência no resultado do outro:
Probabilidade da intersecção: a probabilidade de acontecer A e B é calculada por:
P (A∩B) = P (A) · P (B)
Probabilidade da união: a probabilidade de acontecer A ou B é calculada por:
P (AՍB) = P (A) + P (B) – P (A∩B)
Acesse também: Quatro conteúdos básicos de Matemática para o Enem
Questões sobre probabilidade no Enem
Questão 1 – (Enem) O diretor de um colégio leu numa revista que os pés das mulheres estavam aumentando. Há alguns anos, a média do tamanho dos calçados das mulheres era de 35,5 e, hoje, é de 37,0. Embora não fosse uma informação científica, ele ficou curioso e fez uma pesquisa com as funcionárias do seu colégio, obtendo o quadro a seguir:
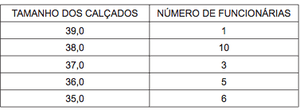
Escolhendo uma funcionária ao acaso e sabendo que ela tem calçado maior que 36,0, a probabilidade de ela calçar 38,0 é:
A) 1/3
B) 1/5
C) 2/5
D) 5/7
E) 5/14
Resolução
Alternativa D
Sempre que falamos de questões do Enem, é necessário muita atenção, mas em probabilidade condicional, de forma específica, o mais importante é identificar bem quem é o seu espaço amostral, pois houve uma restrição desse espaço na questão. Não é necessário usar a fórmula da probabilidade condicional, desde que você consiga encontrar o novo espaço amostral após a restrição.
U: calçar mais que 36
n(U) = 3 + 10 + 1 = 14
A: calçar 38
n(A) = 10
Conhecendo o n(A) e n(U), agora basta calcular a probabilidade:
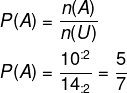
Questão 2 – (Enem 2015 – PPL) No próximo final de semana, um grupo de alunos participará de uma aula de campo. Em dias chuvosos, aulas de campo não podem ser realizadas. A ideia é que essa aula seja no sábado, mas, se estiver chovendo no sábado, a aula será adiada para o domingo. Segundo a meteorologia, a probabilidade de chover no sábado é de 30% e a de chover no domingo é de 25%. A probabilidade de que a aula de campo ocorra no domingo é de:
A) 5,0%
B) 7,5%
C) 22,5%
D) 30,0%
E) 75,0%
Resolução
Alternativa C.
Para que o grupo vá para a aula de campo no domingo, é necessário que chova no sábado e não chova no domingo. Sempre que temos o conectivo e em probabilidade, realizamos o produto entre a probabilidade de cada um desses eventos. Note também que são coisas totalmente independentes, pois chover ou não no sábado não influência na probabilidade de chover no domingo.
Dados os eventos A: chover sábado e B: não chover domingo, queremos que ambos aconteçam, então:
P (A∩B) = P (A) · P (B)
A chance de chover no sábado foi dada: P(A) = 30% = 0,3.
Para encontrar a chance de não chover no domingo, encontraremos a probabilidade complementar. Sabendo-se que a chance de chover domingo é 25%, então a chance de não chover é 100% – 25%, ou seja: P (B) = 75% = 0,75.
Sendo assim, a chance de que os alunos participem dessa aula no domingo é calculada por:
P (A∩B) = P (A) · P (B)
P (A∩B) = 0,3 · 0,75
P (A∩B) = 0,225 = 22,5%