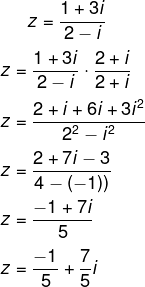Conhecemos como números complexos os números z, que podem ser representados da forma z = a + bi. O conjunto dos números complexos surgiu para ampliar o conjunto dos números reais, já que neste as raízes de números negativos não estavam contidas. Com isso, utilizamos i para representar a unidade imaginária, i = √-1, e, assim, tornou-se mais fácil o desenvolvimento de conceitos e das operações com os números complexos.
Na representação algébrica a + bi, a é conhecido como parte real e b é conhecido como parte imaginária. Existe a representação geométrica de um número complexo, o que pode acontecer no plano complexo, conhecido também como plano de Argand-Gauss. Outra forma de representação de um número complexo é a forma trigonométrica, conhecida também como forma polar.
Leia também: Qual é a origem dos sinais?
Tópicos deste artigo
- 1 - Números complexos
- 2 - Forma algébrica de um número complexo
- 3 - Operações com números complexos
- 4 - Conjugado de um número complexo
- 5 - Plano de Argand-Gauss
- 6 - Módulo de um número complexo
- 7 - Argumento de um número complexo
- 8 - Forma trigonométrica ou polar
- 9 - Exercícios resolvidos
Números complexos

A partir da existência da matemática ao longo dos anos, as ideias envolvendo números foram se adaptando e desenvolvendo as necessidades do ser humano. Com a ideia de números, surgiram vários conjuntos numéricos, são eles:
-
conjunto dos números complexos
Acontece que, na resolução de algumas equações, percebeu-se que o resultado era a raiz de um número negativo, resultado esse que não pertencia a nenhum conjunto antes da criação dos números complexos. Os estudos dos números complexos tiveram grandes contribuições de Giralmo Cardono, Gauss e Argand.
Forma algébrica de um número complexo
Na tentativa de resolver equações quadráticas, é bastante comum que apareça a raiz de um número negativo, por exemplo, a equação x² = -9 não possui solução no conjunto dos números reais, porém, quando se vale de números complexos, é possível representar sua solução.
Para resolver equações que envolvem raízes de números negativos, utilizamos a seguinte representação:
![]()
Então, ao resolvermos a equação x² = -9, temos que:
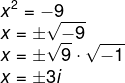
Existem duas soluções para essa equação que são números complexos, x = 3i ou x = -3i.
Todo número complexo z pode ser representado em sua forma algébrica:
z = a + bi
a → parte real
b → parte imaginária
Com a e b pertencentes ao conjunto dos números reais.
Exemplo:
3 + √-4 é um número complexo. Como não é possível calcular a raiz de um número negativo, vamos representar a raiz de -1 por i. Sabemos que a raiz de 4 é 2, logo, esse número será representado por:
z = 3 + 2i
Dependendo do valor de a e de b, existem três casos possíveis para o número complexo, ele pode ser imaginário, imaginário puro ou real.
-
Imaginário
Um número é considerado imaginário quando a sua parte real e a sua parte imaginária são diferentes de zero.
Exemplos:
a) z1 = -1 – 3i
b) z2 = 5 + i
c) z3 = 2 – 4i
d) z4 = -3 + 2i
-
Imaginário puro
Um número complexo é um imaginário puro quando a sua parte real é igual a zero.
Exemplos:
a) z1 = 2i
b) z2 = -3i
c) z3 = 0,5i
d) z4 = -4i
-
Real
Um número complexo é real quando a sua parte imaginária é igual a zero.
Exemplos:
a) 4
b) 2,5
c) √2
d) 7
Veja também: Dicas de Matemática para o Enem
Operações com números complexos
O conjunto dos números complexos possui operações bem definidas, logo, é possível realizar a adição, a subtração, a multiplicação e a divisão entre eles.
-
Adição de dois números complexos
Para fazer a adição de dois números complexos, z1 e z2, basta somar parte real com parte real e parte imaginária com parte imaginária.
Dados: z1 = a + bi e z2 = c + di, então, z1 + z2 = (a + c) + (b + d)i
Exemplo:
z1 = 3 + 5i e z2 = 4 + i, então:
z1 + z2 = (3 + 4) + (5 + 1)i
z1 + z2 = 8 + 5i
-
Subtração de dois números complexos
Para realizar a subtração de z1 – z2, faremos a subtração da parte real pela parte real e da parte imaginária pela parte imaginária.
Exemplo:
z1 = 4 + 2i e z2 = 1 + 4i
z1 – z2 = (4 – 1) + (2 – 4)i
z1 – z2 = 3 – 2i
-
Potências da unidade imaginária
Para compreender a multiplicação entre dois números complexos, antes é necessário entender como calcular a potenciação da unidade imaginária. Note que:
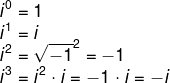
Ao calcular as próximas potências, é possível perceber que o resultado se repetirá:
i4 = i2 · i2 = (-1) (-1) = 1 → i0
i5 = i2 · i3 = (-1) (-i) = i → i1
i6 = i5 · i = i · i = -1 → i²
i7 = i6 · i = (-1) · i = -i → i³
Como a potência é cíclica, para calcular potências maiores, basta realizar a divisão do expoente por 4. Quando realizamos essa divisão, temos como opções de resto 0, 1, 2 ou 3, que será o novo expoente da potência.
Exemplo:
Calcule i35:
Dividindo 35 : 4, temos como quociente 8, pois 8 · 4 = 32, e o resto será 3. Então:
i35 = i3 = -i
-
Multiplicação de números complexos
Para a multiplicação de dois números complexos, vamos aplicar a propriedade distributiva.
Exemplo:
Calcule o produto de (5 + 3i) (2 – 3i):
(5 + 3i) (2 – 2i) = 10 – 15i + 6i – 9i² → sabemos que i² = -1
(5 + 3i) (2 – 2i) = 10 – 15i + 6i – 9 (-1)
(5 + 3i) (2 – 2i) = 10 – 15i + 6i + 9
(5 + 3i) (2 – 2i) = 19 – 9i
Leia também: Quatro conteúdos básicos de Matemática para o Enem
Conjugado de um número complexo
Conhecemos como conjugado de um número complexo escrito da forma a + bi o número complexo a – bi. Utilizamos o conjugado para calcular a divisão de dois números complexos.
![]()
Como não podemos deixar raiz no denominador de uma fração, para realizar a divisão, calculamos:
![]()
Multiplica-se pelo conjugado do denominador, a fim de eliminar a raiz do denominador.
Exemplo:
(6 – 4i) : (4 + 2i)
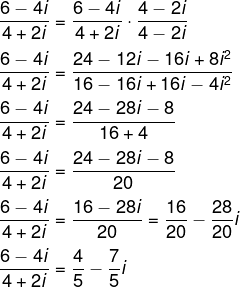
Plano de Argand-Gauss
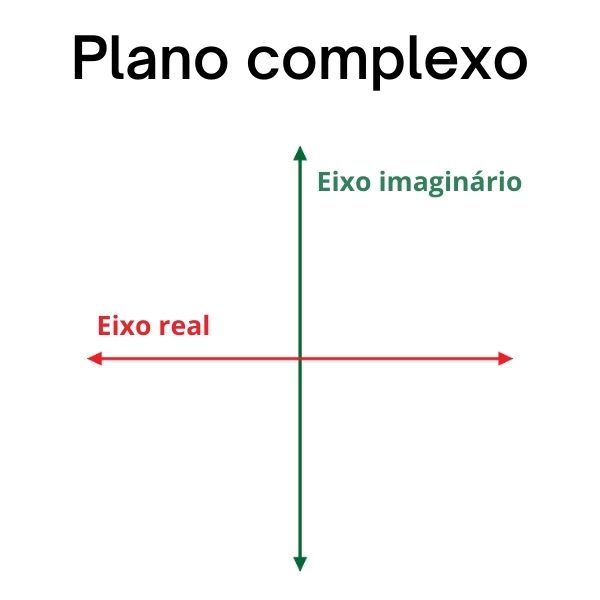
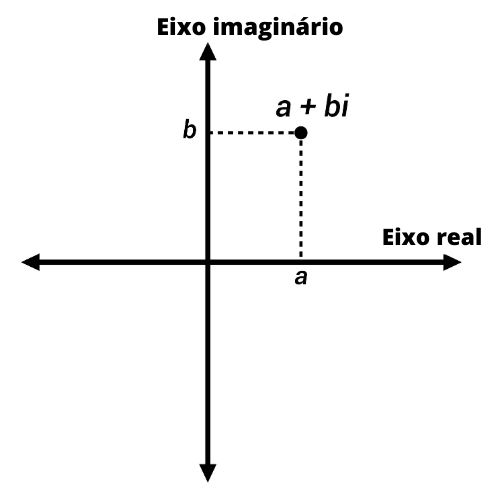
Conhecido também como plano complexo, o plano de Argand-Gauss é uma adaptação do plano cartesiano para a representação de números complexos.
Os números complexos são representados por pontos no plano de Argand-Gauss com coordenadas (a,b). No eixo vertical, representamos a parte imaginária do número, e no eixo horizontal, a parte real.
Módulo de um número complexo
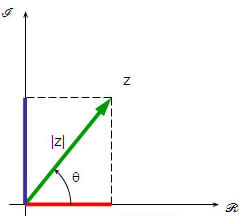
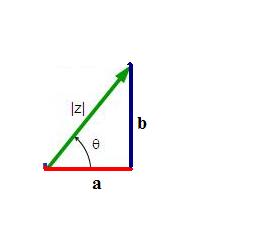
Assim como nos números reais, o módulo de um número complexo está ligado à distância que ele está da origem. Como estamos trabalhando com uma representação em um plano, essa distância é dada pelo teorema de Pitágoras.
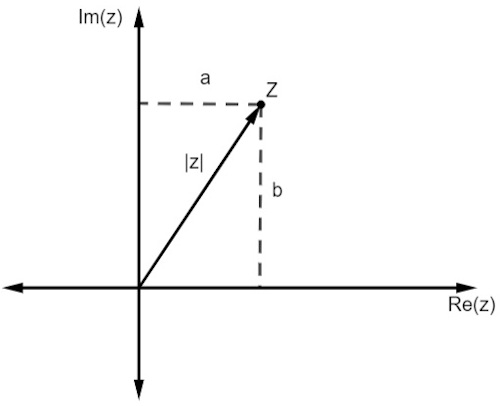
Note que o módulo de z, representado por |z|, é a hipotenusa do triângulo retângulo. Então, temos que:
![]()
Exemplo:
Calcule o módulo de z = 3 + 2i.
|z|² = 3² + 4²
|z|² = 9 + 16
|z|² = 25
|z| = √25
|z| = 5
Veja também: Temas de Matemática que mais caem no Enem
Argumento de um número complexo
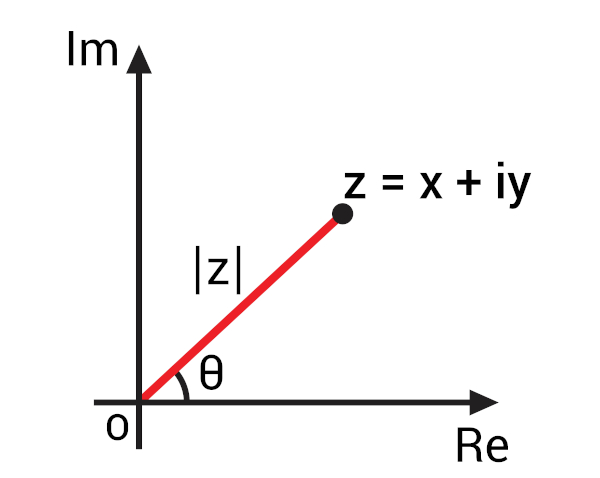
Conhecemos como argumento de um número complexo o ângulo formado entre o eixo horizontal e o seguimento do módulo de z.
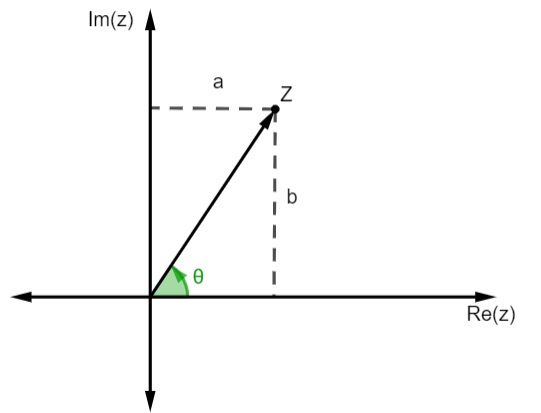
Então, conhecemos como argumento de z o valor do ângulo θ arg (z) = θ. Para encontrar o valor desse ângulo, analisamos o valor do seno e do cosseno do ângulo θ.
Exemplo:
Encontre arg(z) sabendo que z = 1 + √3i.
Primeiro calcularemos |z|, para depois encontrarmos o seno e o cosseno do ângulo:
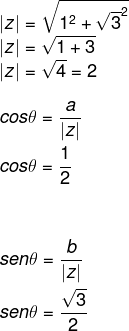
O ângulo que possui esses valores para o cosseno e para o seno é o de 60º, que pode ser representado também como π/3.
Forma trigonométrica ou polar
A forma trigonométrica é uma outra possibilidade de representação para um número complexo. Também é conhecida como forma polar de um número complexo. Analisando a fórmula do cosseno e do seno, podemos reescrever a parte real e a parte imaginária da seguinte forma:
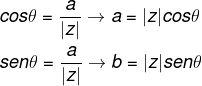
Sabemos que
z = a + bi, então, temos que:
z = |z| cos θ + |z| sen θ · i
Colocando |z| em evidência, encontramos a forma trigonométrica do número:
z = |z|(cos θ + i · sen θ)
Exemplo:
Escreva na forma trigonométrica o número z = 1 + 1i.
Para escrever na forma trigonométrica, precisamos do argumento e do módulo de z.
|z|² = 1² + 1²
|z|² = 1 + 1
|z|² = 2
|z| = √2
Agora vamos calcular o seno e o cosseno do ângulo:
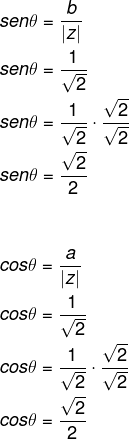
Ao consultar a tabela dos ângulos notáveis, sabemos que o ângulo que possui seno e cosseno com os valores encontrados é θ = 45º. Então, na forma trigonométrica, temos que:
z = |z|(cos θ + i · sen θ)
z = √2(cos 45º + i · sen 45º)
Exercícios resolvidos
Questão 1 – (FAG 2018) Considere a unidade imaginária dos números complexos.
O valor da expressão (i + 1)8 é:
A) 32i
B) 32
C) 16
D) 16i
E) 48
Resolução
Alternativa C
Temos que:
(i + 1)8 = ((i + 1)²)4 = (i² + 2i + 1²)4
(i + 1)8 = (-1 + 2i + 1)4
(i + 1)8 = (2i)4
(i + 1)8 = 24 i4
Sabemos que 4 : 4 = 0, então i4 = i0 = 1.
(i + 1)8 = 16 · 1 = 16
Questão 2 – (Uel) A forma algébrica do número complexo z = (1 + 3i)/(2 – i) é:
A) 1/2 – 3i
B) 5/3 + (7i/3)
C) -1/5 + (7i/5)
D) -1/5 + 7i
E) 3/5 + (4i/5)
Resolução
Alternativa C
Calculando a divisão: