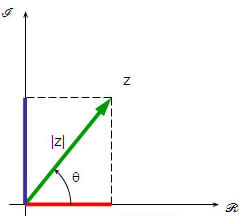
O argumento de um número complexo é o ângulo θ formado pelo eixo da parte real do número complexo e o segmento que liga o número complexo até a origem. Utilizamos o plano de Argand-Gauss para representar números complexos, o número complexo z = x + yi é representado pelo ponto (x, y).
Para encontrar o valor do argumento de um número complexo, denotado por arg(z), utilizamos as razões trigonométricas para calcular o seno do ângulo θ e o cosseno do ângulo θ, conhecendo o valor do seno e do cosseno. Então, consultando a tabela trigonométrica, é possível encontrar o valor do ângulo, ou seja, o valor de θ.
Leia também: Como calcular as potências de i?
Tópicos deste artigo
- 1 - O que é o argumento de um número complexo?
- 2 - Módulo de um número complexo
- 3 - Passo a passo para encontrar o argumento de um ângulo
- 4 - Exercícios resolvidos
O que é o argumento de um número complexo?
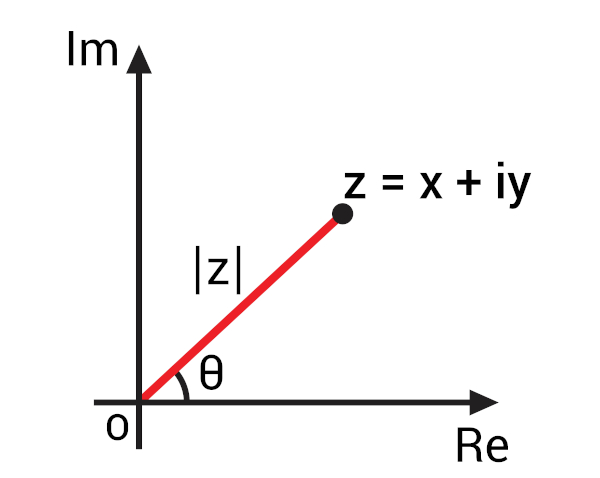
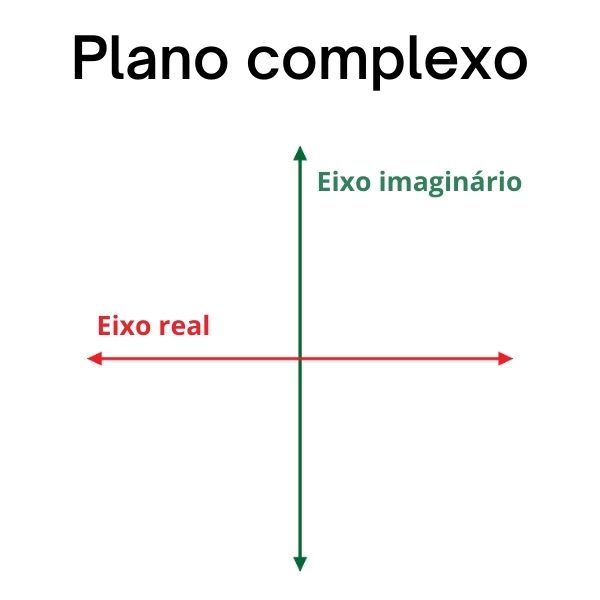
Com a representação de um número complexo no plano de Argand-Gauss, conhecido também como plano complexo, foi possível desenvolver conceitos importantes para os números complexos com base na sua representação geométrica. Com a representação de um número complexo da forma algébrica z = x + yi, podemos representá-lo pelo ponto Z(x, y) no plano complexo. Ao representar esse ponto no plano, podemos traçar o segmento OZ, ou seja, o segmento de reta que liga a origem do plano complexo ao ponto Z.
Esse segmento OZ forma um ângulo com o eixo da parte real, ou seja, o eixo horizontal. Esse ângulo é conhecido como argumento do número complexo z, geralmente representado por arg(z). Para encontrar o argumento do número complexo, vamos recorrer às razões trigonométricas.
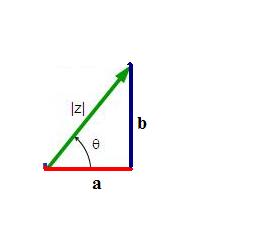
Para conseguir calcular o valor do ângulo θ, antes, precisamos encontrar o valor do módulo desse número complexo, representado na imagem por |z|.
Módulo de um número complexo
No estudo do conjunto dos números reais, o conceito de módulo está ligado à distância que o número real está do zero. Para estender esse conceito para os números complexos, é importante lembrar que, geometricamente, o número completo é um ponto no plano complexo, logo, o módulo de um número complexo é a distância que esse ponto está da origem do eixo. Note na imagem anterior que o módulo |z| é a hipotenusa do triângulo retângulo, então, ele pode ser calculado utilizando o teorema de Pitágoras:
|z|² = x² + y²
Exemplo:
Encontre o módulo do número complexo 5 – 12i.
|z|² = 5² + (-12)²
|z|² = 25 + 144
|z|² = 169
|z| = √169
|z| = 13
Passo a passo para encontrar o argumento de um ângulo
Para encontrar o argumento de um número complexo, temos que:
arg(z) = θ
Aplicando as razões trigonométricas para encontrar o valor do ângulo θ, vamos recorrer às razões trigonométricas seno e cosseno. Temos que:
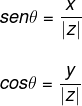
O valor do ângulo pode ser calculado seguindo alguns passos:
- 1º passo: Encontrar o módulo de z.
- 2º passo: Calcular o seno e o cosseno.
- 3º passo: Identificar o valor do argumento com base nos valores de seno e cosseno encontrados.
Exemplo:
Encontre o argumento do número complexo 1 + √3z.
- 1º passo: Calcular |z|.
|z|² = 1² + √3²
|z|² = 1 + 3
|z|² = 4
|z| = √4
|z| = 2
- 2º passo: Calcular o seno e o cosseno de θ.
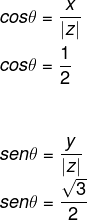
Como o valor de x e y é positivo, então, o ponto está no primeiro quadrante. Consultando a tabela trigonométrica, o valor do ângulo que possui os valores de cosseno e de seno encontrados é igual a:
![]()
Veja também: Operações com números complexos na forma algébrica
Exercícios resolvidos
Questão 1 - O valor do argumento do número complexo z = 1 – i é:
A) 45º
B) 135º
C) 235º
D) 315º
E) 350º
Resolução
Alternativa D
1º passo: Calcular o |z|.
|z|² = 1² + (-1)²
|z|² = 1 + 1
|z|² = 2
|z| = √2
2º passo: Calcular o cosseno de θ.
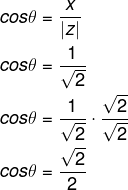
Calcular também o seno de θ:
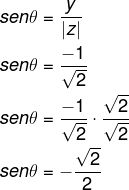
O ângulo que possui os valores do seno e do cosseno encontrados é um ângulo do 4º quadrante, pois x é positivo e y é negativo. Note, pelos valores de seno e cosseno, que esse ângulo é congruente ao ângulo de 45º no quarto quadrante θ: 360 – 45 = 315º.
Questão 2 - A forma algébrica do número complexo z, sabendo que arg(z) = 120º e |z| = 2√3, é:
A) z = – 3 + √3i
B) z = 3 + √3i
C) z = √3 + 3i
D) z = √3 – 3i
E) z = – √3 + 3i
Resolução
Alternativa E
Sabemos que 120º é um ângulo do 2º quadrante congruente a 60º. Pelo cosseno e o seno, temos que:
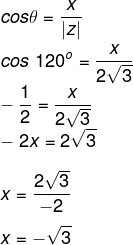
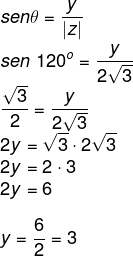
Então, o número complexo é z = – √3 + 3i.