Forma trigonométrica de um número complexo

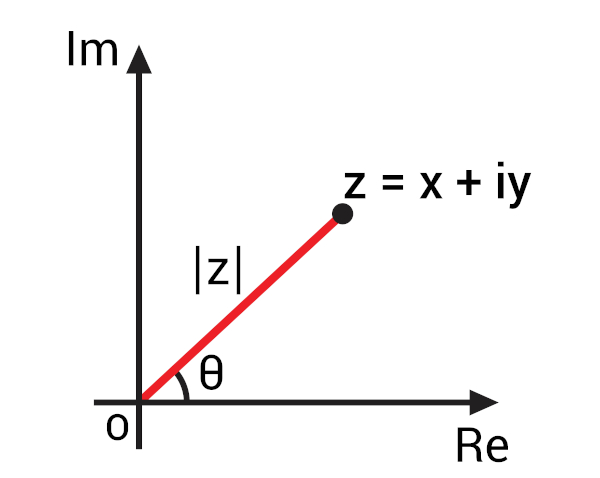
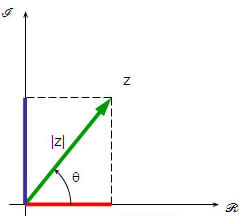
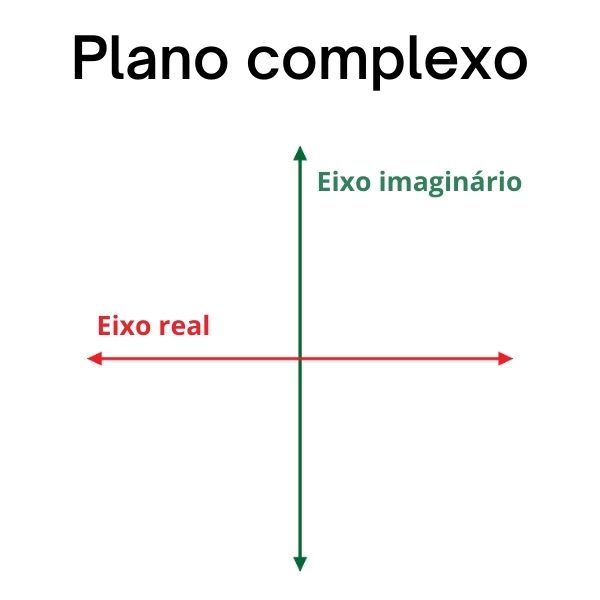
Número complexo é um par ordenado de números reais z= (a, b). Na forma algébrica, o par ordenado pode ser escrito como z = (a + bi). Representando um número complexo no plano de Argand-Gauss, obtemos:

Onde:
|z| → é o módulo do número complexo z.
θ → é o argumento de z.

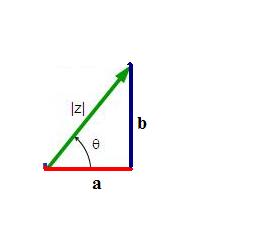
Pelo teorema de Pitágoras, obtemos:

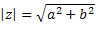
Podemos escrever a e b em função de θ e |z| utilizando a trigonometria no triângulo retângulo.

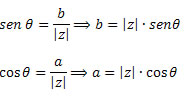
Substituindo as duas igualdades acima na forma algébrica de z, teremos:

z = |z|∙cosθ + |z|∙senθ∙i

Colocando |z| em evidência, obtemos:

z = |z|(cosθ + i∙sen θ) → que é chamada de forma trigonométrica de z ou forma polar.

A forma trigonométrica é muito utilizada na potenciação e radiciação de números complexos, que são objetos de estudos futuros no conjunto complexo.

Vejamos alguns exemplos para melhor compreensão.

Exemplo 1: Escreva cada um dos seguintes números complexos na forma trigonométrica.

a) z = 1 + i

Solução: Pela forma algébrica, temos que:
a = 1 e b = 1

Segue que:

Assim, obtemos:

Como o ponto (a, b) = (1, 1) está no primeiro quadrante, podemos afirmar que o ângulo θ que apresenta os valores de seno e cosseno indicados acima é θ = 45^o. Dessa maneira, a forma trigonométrica do número complexo será:
z = √2 (cos45^o + i∙sen 45^o )

b) z = -1 + i√3

Solução: A partir da forma algébrica, obtemos:

a = -1 e b = √3

O módulo de z será dado por:

Segue que:

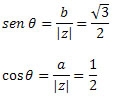
Como o ponto (a, b) = (-1,√3) pertence ao segundo quadrante, podemos afirmar que o ângulo θ que apresenta os valores de seno e cosseno indicados é θ = 120o. Logo, a forma trigonométrica ou polar do número complexo será:

z = 2(cos120^o + i∙sen 120^o)

Exemplo 2. Obtenha a forma algébrica do número complexo
z = 6(cos270^o + i∙sen 270^o )

Solução: Da trigonometria no ciclo, temos que:

cos 270^o = 0 e sen 270^o = – 1

Assim, obtemos:

z = 6(cos270^o + i∙sen 270^o) = 6[0+i∙(-1)] = -6i

Portanto, a forma algébrica de z é z = – 6i