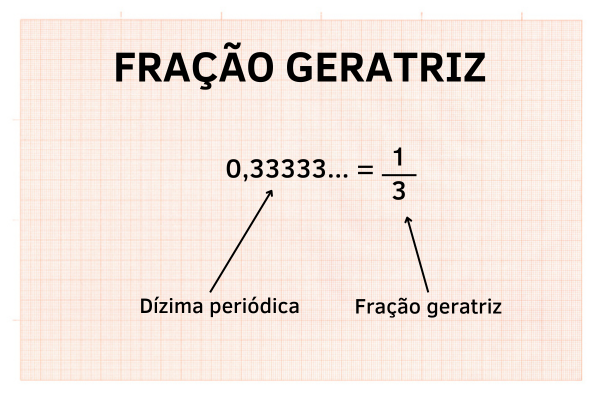
Fração geratriz é a representação fracionária de uma dízima periódica. A fração um terço, por exemplo, é a fração geratriz da dízima 0,3, pois 1 dividido por 3 resulta em 0,333.... Neste texto vamos descobrir como encontrar a função geratriz a partir de uma dízima periódica.
Leia também: Como fazer operações com conjuntos?
Tópicos deste artigo
- 1 - Resumo sobre fração geratriz
- 2 - O que é fração geratriz?
- 3 - O que são dízimas periódicas?
- 4 - Como encontrar a fração geratriz?
- 5 - Método prático para encontrar fração geratriz
- 6 - Exercícios resolvidos sobre fração geratriz
Resumo sobre fração geratriz
-
A geratriz é a fração que representa uma dízima periódica.
-
Dízima periódica é um número com infinitas casas decimais em que certos algarismos se repetem.
-
Os algarismos que se repetem infinitamente compõem o período da dízima.
-
A dízima periódica simples é a que possui, logo após a vírgula, os algarismos periódicos.
-
A dízima periódica composta apresenta uma parte não periódica, após a vírgula, chamada de antiperíodo, que antecede a parte periódica.
O que é fração geratriz?
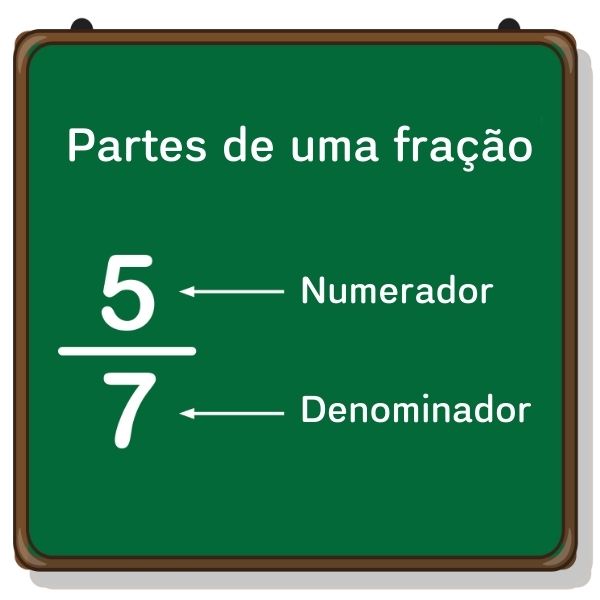
A representação fracionária de uma dízima periódica é chamada de fração geratriz. Assim, o quociente entre o numerador e o denominador é a dízima periódica.
Exemplos:
\(\frac{8}9\) é a fração geratriz de 0,8888…
\(\frac{15}{99}\) é a fração geratriz de 0,151515…
\(\frac{346}{990}\) é a fração geratriz de 0,3494949…
O que são dízimas periódicas?
Dízima periódica é um número cuja representação decimal possui infinitas casas decimais periódicas. Isso significa que, na parte decimal, determinados algarismos se repetem infinitamente. Esses algarismos compõem o período da dízima.
Para indicar que certos dígitos se repetem infinitamente, podemos utilizar o símbolo de reticências ou desenhar um traço acima do período.
Exemplos:
\(0,888…=0, \overline{8}\) é uma dízima periódica de período 8.
\(1,151515…=1, \overline{15}\) é uma dízima periódica de período 15.
\(0,34949494…=0,3 \overline{49}\) é uma dízima periódica de período 49.
Note que, no último exemplo, há um algarismo após a vírgula que não se repete: o 3. Esse algarismo recebe o nome de antiperíodo.
Dízimas periódicas que não possuem antiperíodo são chamadas de simples. É o caso das dízimas \(0,\overline{8}\) e \(1,\overline{15}\) nos exemplos anteriores. Já as dízimas periódicas que possuem antiperíodo, como a \(0,3\overline{49}\), são chamadas de compostas.
Toda dízima periódica é um número racional. Consequentemente, toda dízima periódica — simples ou composta — pode ser expressa por uma fração com numerador e denominador inteiros. Dizemos que essa fração é a geratriz da dízima.
Veja também: O que são frações equivalentes?
Como encontrar a fração geratriz?
Uma maneira de determinar a fração geratriz de uma dízima periódica é montar uma equação em que a incógnita é a fração procurada. Vejamos como fazer isso tanto para dízimas periódicas simples como para as compostas.
→ Passo a passo para encontrar fração geratriz de dízima simples
O procedimento para encontrar a fração geratriz de uma dízima periódica simples é formado por 3 passos:
Passo 1: Igualar a dízima a uma incógnita (como x).
Passo 2: Multiplicar os dois lados da igualdade por \(10^p\), em que p é a quantidade de algarismos no período.
Passo 3: Subtrair a equação do passo 2 pela equação do passo 1.
A partir disso, o valor da incógnita será a fração geratriz buscada.
Exemplo:
Determine a fração geratriz de \(8,\overline{6}\).
Passo 1:
x = 8,666666666….
Passo 2: Como o período é formado por apenas um algarismo (6), multiplicamos os dois lados da igualdade por 10.
10x = 86,666666666…
Passo 3: Subtraímos a equação do passo 2 pela equação do passo 1. Perceba que, com esse passo, conseguimos remover a parte infinita da dízima periódica.
\(10x - x = 86,\color{red}{666666666…} - 8,\color{red}{666666666…}\)
\(9x = 86 - 8\)
\(9x = 78\)
\(x=\frac{78}9\)
Dessa forma, \(\frac{78}8\) é a fração geratriz da dízima 8,666....
-
Videoaula sobre fração geratriz de dízimas periódicas simples
→ Passo a passo para encontrar fração geratriz de dízima composta
No caso das dízimas periódicas compostas, o processo é muito semelhante, porém com uma etapa a mais no início do passo 2 e uma alteração nas equações subtraídas no passo 3:
Passo 2 (dízimas compostas): Multiplicar os dois lados da igualdade por \(10^a\), em que a é a quantidade de algarismos no antiperíodo, e multiplicar os dois lados da igualdade por \(10^p\), em que p é a quantidade de algarismos no período.
Passo 3 (dízimas compostas): Subtrair as equações obtidas no passo 2.
Observe o exemplo.
Exemplo:
Determine a função geratriz de \(6,4\overline{85}\).
Passo 1:
x = 6,4858585…
Passo 2: Como o antiperíodo possui um algarismo (4), primeiro multiplicamos os dois lados por 10:
10x = 64,858585…
Depois, considerando que o período possui dois algarismos (85), multiplicamos os dois lados por \(10^2\):
1000x = 6485,858585…
Passo 3: Ao subtrair as equações do passo 2, podemos eliminar a parte decimal infinita da dízima periódica.
\(1000x -10x= 6485,\color{red}{858585…} - 64,\color{red}{858585…}\)
\(990x = 6485 - 64\)
\(990x = 6421\)
\(x=\frac{6421}{990}\)
Portanto, \(\frac{6421}{990}\) é a fração geratriz de 6,4858585....
-
Videoaula sobre fração geratriz de uma dízima periódica composta
Método prático para encontrar fração geratriz
O método prático é um “atalho” para o raciocínio que fizemos antes, um caminho direto para obter a fração geratriz de uma dízima periódica (simples ou composta).
Vejamos como realizar esse método em cada caso.
→ Método prático para dízimas simples
Passo 1: Escreva a dízima como uma soma entre a parte inteira e a parte decimal.
Passo 2: Escreva a parte decimal como uma fração em que o numerador é o período e o denominador é formado por p noves, em que p é a quantidade de algarismos no período.
Exemplo:
Aplique o método prático para obter a geratriz de \(4,\overline{5}\).
Passo 1:
\(4,\overline{5} = 4 + 0,555…\)
Passo 2: Como o período é formado por apenas um algarismo (5), o denominador terá apenas um 9.
\(4,\overline{5}=4+\frac{5}9\)
\(4,\overline{5}=\frac{41}9\)
Assim, \(\frac{41}9\) é a fração geratriz de 4,555...
→ Método prático para dízimas compostas
No caso da dízima composta, o método envolve construir a fração geratriz do seguinte modo:
-
O numerador é uma subtração em que o primeiro termo é composto pela parte inteira, o antiperíodo e um período (nessa ordem) e o segundo termo é a parte inteira e o antiperíodo.
-
O denominador é formado por p noves, em que p é a quantidade de algarismos no período, seguido de a zeros, em que a é a quantidade de algarismos no antiperíodo.
Exemplo:
Aplique o método prático para obter a geratriz de \(3,5\overline{97}\).
A parte inteira é 3, o antiperíodo é 5 e o período é 97. Assim, o primeiro termo do numerador é 3597 e o segundo termo do numerador é 35.
Ainda, como o período possui dois algarismos e o antiperíodo possui um algarismo, o denominador é 990.
Portanto, a fração geratriz de 3,5979797... é:
\(\frac{3597-35}{990}\)
Portanto:
\(3,5979797..=\frac{3562}{990}\)
Saiba mais: 3 macetes matemáticos para usar na prova do Enem
Exercícios resolvidos sobre fração geratriz
Questão 1
(Enem) Um estudante se cadastrou numa rede social na internet que exibe o índice de popularidade do usuário. Esse índice é a razão entre o número de admiradores do usuário e o número de pessoas que visitam seu perfil na rede. Ao acessar seu perfil hoje, o estudante descobriu que seu índice de popularidade é 0,3121212…
O índice revela que as quantidades relativas de admiradores do estudante e pessoas que visitam seu perfil são
a) 103 em cada 330.
b) 104 em cada 333.
c) 104 em cada 3333.
d) 139 em cada 330.
e) 1039 em cada 3330.
Resolução
x = 0,3121212…
Como 0,3121212… é uma dízima periódica composta:
10x = 3,121212…
1000x = 312,121212…
Assim:
\(1000x - 10x = 312,\color{red}{121212…} - 3,\color{red}{121212…}\)
\(990x = 312 – 3\)
\(990x=309\)
\(x=\frac{309}{990}\)
Simplificando a fração ao dividir o numerador e denominador por 3:
\(x=\frac{103}{330}\)
Alternativa A
Questão 2
(PUC) O valor de \(\frac{\sqrt{1,777…}}{\sqrt{0,111…}}\) é:
a) 4,444...
b) 4
c) 4,777...
d) 3
e) \(\frac{4}3\)
Resolução
Primeiro encontramos a geratriz das dízimas nos radicandos e depois substituímos na expressão original.
\(1,777… = 1 + 0,777…\)
\(1,777…=1+\frac{7}9\)
\(1,777…=\frac{16}9\)
Ainda:
\(0,111…=\frac{1}9\)
Logo:
\(\frac{\sqrt{1,777…}}{\sqrt{0,111…}} = \frac{\sqrt{\frac{16}{9}}}{\sqrt{\frac{1}{9}}}\)
\(\frac{\sqrt{1,777…}}{\sqrt{0,111…}} = \frac{\frac{4}{3}}{\frac{1}{3}}\)
\(\frac{\sqrt{1,777…}}{\sqrt{0,111…}} = 4\)
Alternativa B