O princípio de Cavalieri foi desenvolvido para facilitar o cálculo do volume dos sólidos geométricos. Existem alguns sólidos que possuem formas que dificultam o cálculo do seu volume. Para facilitar essa tarefa, Cavalieri recorreu à comparação de volumes entre sólidos conhecidos.
O princípio desenvolvido por esse estudioso diz que, se existem dois sólidos geométricos de mesma altura, ao cortá-los com um plano paralelo à base, em qualquer altura dos sólidos, se a área da intersecção com os dois sólidos for sempre a mesma, então esses sólidos terão volumes iguais.
Veja também: Ponto, reta, plano e espaço: conceitos basilares do estudo da geometria
Tópicos deste artigo
- 1 - Definição do princípio de Cavalieri
- 2 - Volume do cilindro com o princípio de Cavalieri
- 3 - Volume da esfera
- 4 - Exercícios resolvidos
Definição do princípio de Cavalieri

O matemático italiano Bonaventura Francesco Cavalieri realizou estudos para o cálculo do volume de sólidos geométricos. Durante seus estudos, ele publicou o método do indivisível, que hoje é conhecido como princípio de Cavalieri.
Por meio da comparação entre sólidos geométricos, o princípio de Cavalieri diz que dois sólidos geométricos que possuem a mesma altura terão o mesmo volume se as figuras planas formadas pelas secções planas paralelas à base, em qualquer altura dos sólidos geométricos, tiverem sempre a mesma área.

Analisando os prismas da imagem, é possível perceber que as figuras formadas no encontro do sólido com o plano ▯ são polígonos com formatos diferentes. Se eles possuem mesma área e mesma altura, então, pelo princípio de Cavalieri, esses sólidos possuem o mesmo volume.
Com base nos estudos de Cavalieri, foi possível desenvolver uma fórmula para calcular o volume de qualquer prisma. Como essa figura pode ter uma base no formato de qualquer polígono, para calcular o volume do prisma, utilizamos a seguinte fórmula:
V = Ab × h
V → volume
Ab → área da base
h → altura
A área é calculada de acordo com o formato da base, ou seja, de acordo com o polígono que a forma.
Leia também: Quais são as principais diferenças entre figuras planas e espaciais?
Volume do cilindro com o princípio de Cavalieri
Utilizando a comparação de um prisma com um cilindro, foi possível perceber que o volume do cilindro também pode ser calculado de forma parecida com o volume de um prisma, ou seja, por meio do produto da base pela altura.
Legenda: Princípio de Cavalieri na comparação do prisma com o cilindro.
Dado um cilindro, é possível encontrar um prisma com o mesmo volume do cilindro, desde que a área da base desse prisma seja congruente à área do cilindro, o que tornou possível perceber que o volume do cilindro também é o produto da base pela altura.
V = Ab × h
A base do cilindro é sempre igual a um círculo, e sabemos que a área do círculo é calculada por πr². Sendo assim, em um cilindro, o volume será calculado pela fórmula:
V = πr² × h
Volume da esfera
A fórmula para calcular o valor do volume da esfera pode ser encontrada por meio do princípio de Cavalieri. Na busca de um sólido em que fosse possível aplicar esse princípio, foi encontrada a figura conhecida como anticlépsidra.
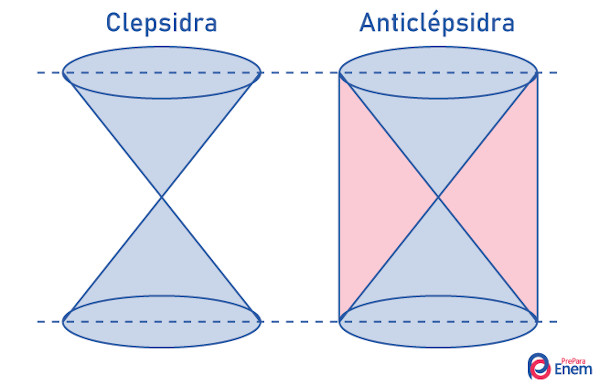
Veja que a clepsidra é formada por dois cones, que possuem altura igual ao raio da sua base. Colocando um cilindro que contém os dois cones, conhecemos como anticlépsidra o sólido formado pela subtração entre volume do cilindro e o volume dos dois cones. Na imagem, é a região destacada em azul. Como queremos comparar essa figura com uma esfera de raio r, então a altura da anticlépsidra tem que ser igual a 2r. Logo, temos que:
V = Vcilindro – 2 Vcone
Então:
Vcilindro = πr²·h
Como h = 2r, chegamos a:
Vcilindro = πr²·2r
Vcilindro = 2 πr³
Já o volume de um cone qualquer é:
![]()
Vale dizer que h é a altura do cone e, nesse caso, a altura dele é igual a r, já que a altura é a metade da altura da anticlépsidra, portanto:

O volume da anticlépsidra é igual a:

Conhecendo o volume da anticlépsidra, vamos compará-lo com o da esfera. Acontece que, ao utilizarmos o princípio de Cavalieri, é possível perceber que a anticlépsidra possui a mesma altura da esfera, ou seja, h = 2r. Além disso, ao realizarmos secções nesses sólidos geométricos, é possível demonstrar que a área da circunferência formada na secção da esfera sempre será congruente à área da coroa formada na secção da anticlépsidra.
Analisando um plano α que intercepta os dois sólidos geométricos, é possível provar que as áreas são iguais.
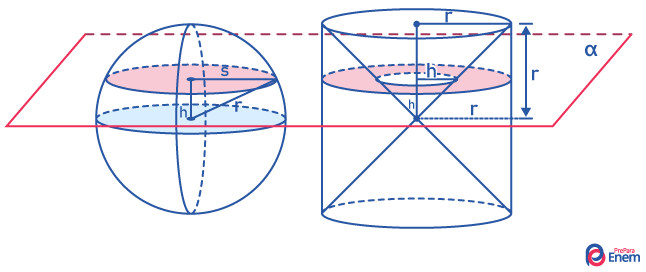
Ao interceptar a esfera, a intersecção do plano com a esfera é um círculo de raio s. A área desse círculo é calculada por:
Acírculo = πs²
Já a intersecção do plano com a anticlépsidra forma uma região que chamamos de coroa. A área da coroa é igual à área da circunferência maior menos a área da circunferência menor.
Acoroa = πr² - πh²
Acoroa = π (r² – h² )
Analisando a imagem da esfera, é possível perceber que há um triângulo retângulo que relaciona h, s e r.
r² = s² +h²
Se substituirmos r² por s² +h² na área da coroa, chegaremos a:
Acoroa = π (r² – h² )
Acoroa = π (s² + h² – h² )
Acoroa = π s² = Acírculo
Como as áreas possuem a mesma medida, e as figuras, a mesma altura, então o volume da esfera e da anticlépsidra é igual. Como conhecemos o volume da anticlépsidra, então, para calcular o volume da esfera, podemos usar a mesma fórmula, ou seja:
![]()
Acesse também: Circunferência e círculo: definições e diferenças básicas
Exercícios resolvidos
Questão 1 – (Enem 2015) Para resolver o problema de abastecimento de água foi decidida, numa reunião do condomínio, a construção de uma nova cisterna. A cisterna atual tem formato cilíndrico, com 3 m de altura e 2 m de diâmetro, e estimou-se que a nova cisterna deverá comportar 81 m³ de água, mantendo o formato cilíndrico e a altura da atual. Após a inauguração da nova cisterna. a antiga será desativada.
Utilize 3,0 como aproximação para π.
Qual deve ser o aumento, em metros, no raio da cisterna para atingir o volume desejado?
A) 0,5
B) 1,0
C) 2,0
D) 3,5
E) 8,0
Resolução
Alternativa C.
A nova cisterna tem a mesma altura que a anterior, ou seja, 3 m de altura. Chamaremos de r o raio da nova cisterna. Como ela deve ter 81 m³, então:

Comparando com a cisterna antiga, sabemos que ela tinha 2 metros de diâmetro, ou seja, 1 metro de raio, o que significa que o raio aumentou 2 metros em relação ao raio da antiga cisterna.
Questão 2 - Um reservatório no formato de um prisma de base retangular tem base com 3 metros de comprimento, 4 metros de largura e 2 metros de profundidade. Sabendo que ele está preenchido até a metade, então o volume do reservatório que está ocupado é:
A) 5 m³.
B) 6 m³.
C) 10 m³.
D) 12 m³.
E) 24 m³.
Resolução
Alternativa D.
Para calcular o volume de um prisma, basta multiplicar a área da base pela altura. Como a base é retangular, então:
V = 3 · 4 · 2
V = 24 m³
Como ele está com a metade do seu volume ocupada, então basta dividir o volume total por dois.
24 : 2 = 12 m³








