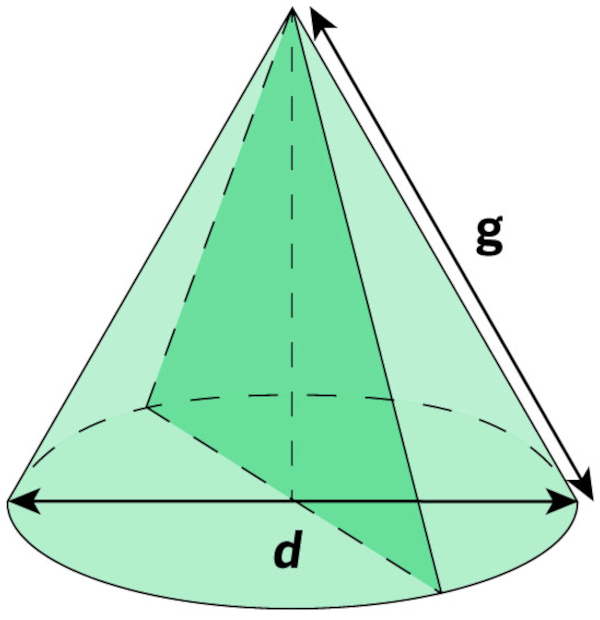
O cone é um sólido geométrico pertencente à classe dos corpos redondos, assim como a esfera e o cilindro. Ele é definido como a união de todos os segmentos de reta com extremidades em um círculo e em um ponto fora dele. Dentre seus elementos, é possível destacar a sua base (que é um círculo), sua altura (distância de seu vértice até sua base) e sua geratriz (distância entre seu vértice e um ponto da circunferência de sua base).
Como alguns outros sólidos geométricos, ele pode ser classificado como reto e oblíquo, além de ser possível determinar uma fórmula para calcular suas áreas superficiais e seu volume.
Leia também: Cilindro — outro sólido geométrico pertencente à classe dos corpos redondos
Tópicos deste artigo
- 1 - Resumo sobre cone
- 2 - O que é cone?
- 3 - Elementos do cone
- 4 - Classificação do cone
- 5 - Fórmulas do cone
- 6 - Tronco de cone
- 7 - Exercícios resolvidos sobre cone
Resumo sobre cone
- O cone é um corpo redondo.
- É definido pela união de segmentos com extremidades em um círculo e em um ponto exterior a ele.
- Sua base é um círculo.
- A geratriz, um de seus principais elementos, é a distância entre seu vértice e a circunferência de sua base.
- Pode ser classificado em cone reto e oblíquo.
- Um cone de revolução é obtido pela rotação de um triângulo retângulo em torno de um de seus catetos.
- Um cone equilátero possui a mesma medida de geratriz e de diâmetro do círculo da base.
- A área total do cone é dada por: \(A=\pi r\left(g+r\right).\)
- O volume do cone é dado por: \(V=\frac{\pi r^2h}{3}\).
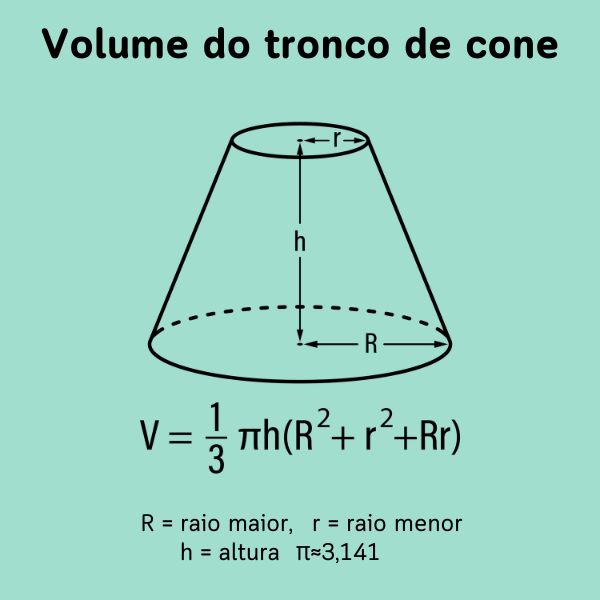
- O tronco de cone é o sólido geométrico formado pela parte de baixo de um cone a partir da secção desse cone feita por um plano paralelo à sua base. Ele apresenta duas bases paralelas.
- O volume do tronco de cone é dado por: \(\frac{\pi h}{3}\left(R^2+Rr+r^2\right).\)
O que é cone?
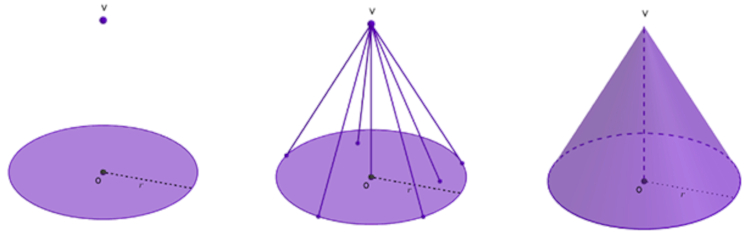
O cone é definido como a união de todos os segmentos de reta com extremidades em um círculo e em um ponto fora dele. Considere um círculo de centro O e raio de medida r. Além disso, considere um ponto V no espaço que não pertence ao círculo. Dizemos que um cone é a reunião de todos os segmentos de reta cujas extremidades são o vértice V e algum ponto do círculo.
Cones de trânsito, chapéus de aniversário, casquinhas de sorvete e muitos outros objetos possuem forma similar a um cone, assim, é possível entender a importância de seu estudo para nosso cotidiano.
Elementos do cone
Veja, a seguir, alguns dos principais elementos do cone:
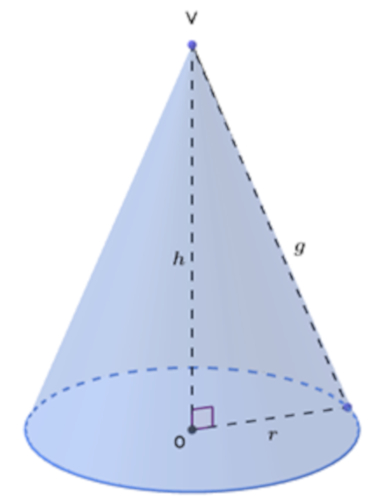
- Vértice (V): O vértice de um cone é o ponto fora do círculo da base que serve como extremidade dos segmentos que formam esse sólido.
- Base: A base do cone é um círculo de centro O e raio de medida r.
- Raio (r): O raio de um cone é a medida do raio do círculo da base.
- Altura (h): A altura do cone é um segmento perpendicular ao plano que contém o círculo da base e representa a distância entre o vértice do cone e esse plano.
- Geratriz (g): A geratriz é o segmento cujas extremidades são o vértice do cone e os pontos da circunferência de sua base.
Classificação do cone
Um cone pode ser classificado de acordo com o segmento VO, que une o vértice do cone com o centro do círculo da base.
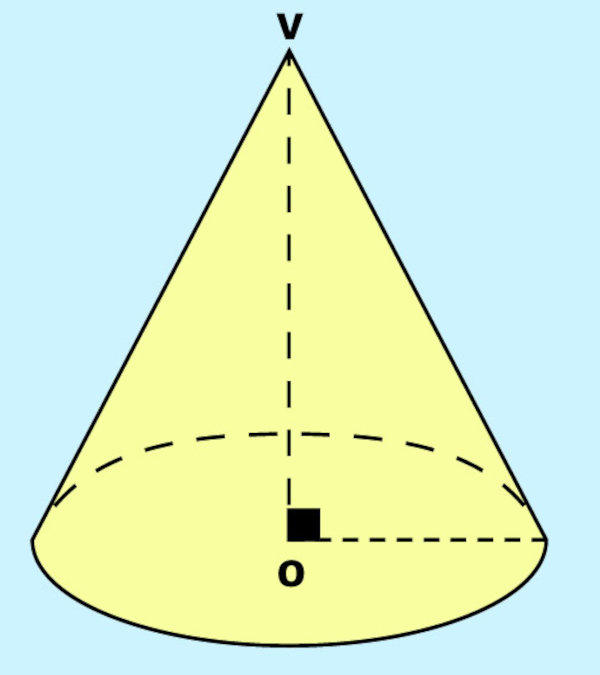
→ Cone reto
Cone reto é o cone em que o segmento VO é perpendicular ao plano da base no qual o círculo está contido. Em outras palavras, se a altura do cone coincidir com a medida do segmento VO, esse cone é dito reto.
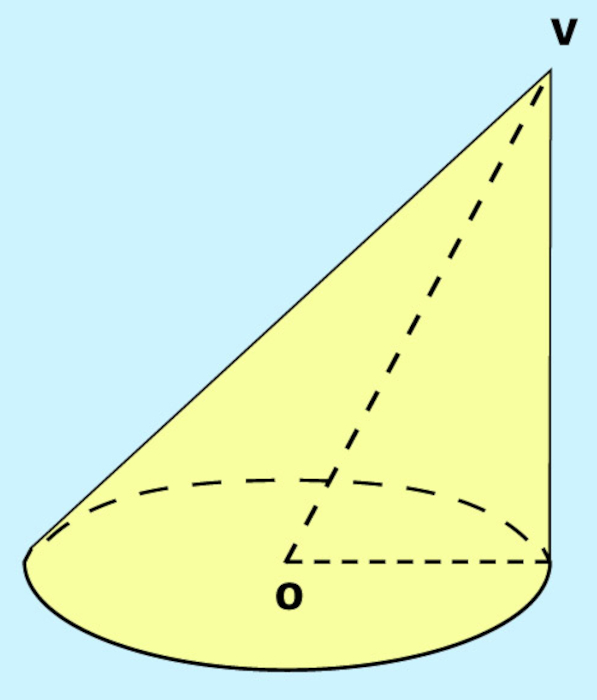
→ Cone oblíquo
Cone oblíquo é o cone que não é reto, ou seja, ele é classificado assim quando o segmento VO não for perpendicular ao plano da base no qual o círculo está contido.
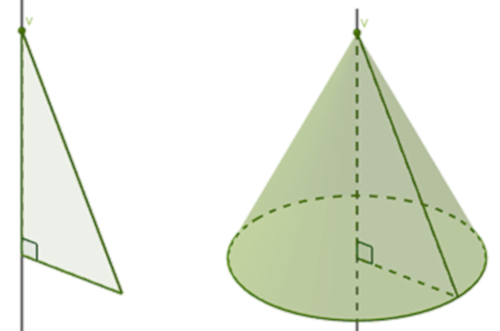
→ Cone de revolução
Cone de revolução é o cone reto obtido pela rotação de um triângulo retângulo em torno de um eixo que contém algum de seus catetos.
→ Cone equilátero
Há ainda uma última classificação de cones, sendo que ela não está relacionada ao segmento VO do cone, mas sim ao diâmetro do círculo de sua base e sua geratriz. O cone equilátero é o cone em que sua geratriz (g) e o diâmetro (d) do círculo da base possuem a mesma medida.
Fórmulas do cone
Da mesma forma que outros sólidos geométricos, o cone possui fórmulas que determinam a área da sua superfície, sua capacidade volumétrica e, ainda, no caso específico do cone, o volume de seu tronco. Veja essas fórmulas a seguir.
→ Fórmulas das áreas do cone
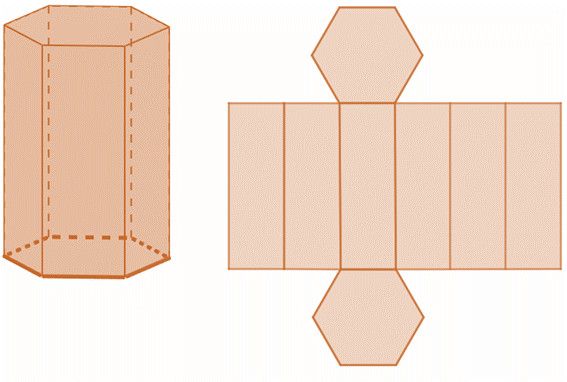
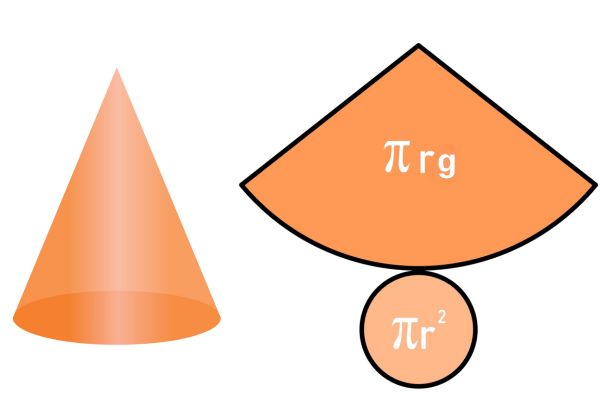
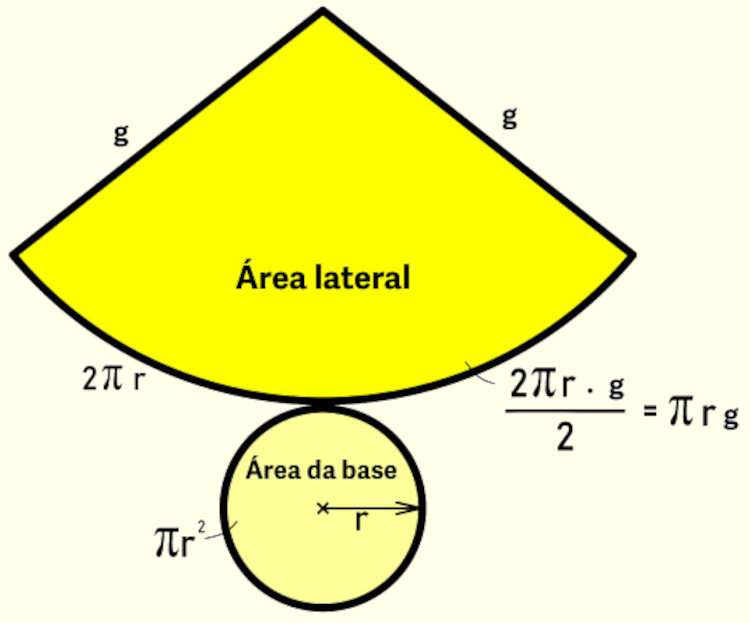
Para analisar a área da superfície total de um cone reto, é preciso analisar as figuras planas que compõem sua planificação. No caso de um cone reto, sua planificação é a seguinte:
◦ Fórmula da área lateral do cone
Para calcular a área lateral do cone, perceba que sua planificação mostra que ela corresponde a um setor circular de raio g e comprimento de arco igual a \(2\pi r\), em que r é o raio do círculo da base. Assim, a área do setor circular em função do comprimento do arco implica que a área lateral do cone é dada por:
Área lateral \(A_l=\pi rg\)
◦ Fórmula da área da base do cone
A área da base do cone é equivalente à área de um círculo de raio r, ou seja:
Área da base \(A_b=\pi r^2\)
◦ Fórmula da área superficial total do cone
A área superficial total do cone é dada por:
Área total \(A_l+A_b=\pi rg+\pi r^2=\pi r\left(g+r\right)\)
→ Fórmula do volume do cone
O volume de um cone é dado por um terço do produto da área da base dele pela sua altura, ou seja:
Volume V = \(V=\frac{1}{3}A_b\cdot h\)
Volume = \(\frac{\pi r^2h}{3}\)
É importante destacar que o volume do cone é o mesmo, não importando sua classificação. Assim, se um cone reto e um cone oblíquo, por exemplo, possuem a mesma altura e a mesma área da base, então a medida de seus volumes também será a mesma.
Tronco de cone
Considere um cone e um plano paralelo à sua base que o intersecta. Dizemos que a região de contato é uma secção do plano com o cone, e, nesse caso, essa intersecção é representada por um círculo. Com base nesse corte feito, é possível destacar a origem do sólido geométrico conhecido como tronco de cone, composto de duas bases, cujos formatos são círculos.
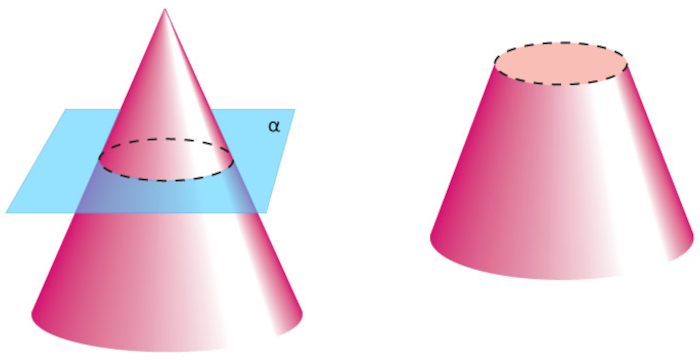
É possível calcular o volume desse tronco de cone sabendo a medida dos raios de seus dois círculos e também a sua altura.
Assim, se h é a altura do tronco de cone, R é o raio do círculo da base maior e r é o raio do círculo da base menor, o volume do tronco de cone é dado por:
Volume do tronco de cone = \(\frac{\pi h}{3}\left(R^2+Rr+r^2\right)\)
Veja também: Como é formado o tronco de pirâmide?
Exercícios resolvidos sobre cone
Questão 1
Um cone reto possui uma geratriz de medida 5cm e o círculo de sua base possui um raio de medida 3cm. O volume desse cone é igual a:
A) \(4\pi cm^3\)
B) \(8\pi cm^3 \)
C) \(12\pi cm^3\)
D) \(16\pi cm^3\)
Resolução:
Alternativa C
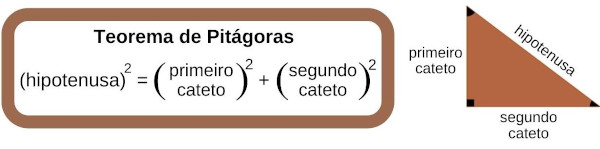
Sabe-se que o cone é reto e, por conta disso, sua geratriz, o raio do círculo de sua base e sua altura relacionam-se, respectivamente, com a hipotenusa e os catetos de um triângulo retângulo.
Assim, pelo teorema de Pitágoras, sabendo a medida de sua geratriz e do raio, é possível encontrar a medida de sua altura:
\(altura=4cm\)
Por fim, sabendo a altura do cone, é possível determinar seu volume:
\(Volume=\frac{\pi r^2h}{3}\)
\(Volume=\frac{\pi3^24}{3}\)
\(Volume=12\pi cm^3\)
Questão 2
(PUC) Um monte de areia tem a forma de um cone circular reto, com volume \(V=4\pi m^3\). Se o raio da base é igual a dois terços da altura desse cone, pode-se afirmar que a medida da altura do monte de areia, em metros, é:
A) 2
B) 3
C) 4
D) 5
Resolução:
Alternativa B
Pela fórmula do volume de um cone, sabemos que:
\(V=\frac{\pi r^2h}{3}\)
Agora, sabendo que \(V=4\pi \) e que \(r=\frac{2}{3}h\), podemos encontrar o valor da altura fazendo:
\(4\pi=\frac{\pi r^2h}{3}\)
\(12\pi=\pi\left(\frac{2}{3}h\right)^2\cdot h\)
\(12=\frac{4}{9}h^2\cdot h\)
\(h^3=27\rightarrow h=3m\)
Fontes
ALMEIDA, Célio Pinto de. Geometria espacial. 1. ed. Rio de Janeiro: G. Ermakoff, 2018.
DOLCE, Osvaldo; NICOLAU, José. Fundamentos de matemática elementar: Geometria espacial, v. 10. 5. ed. Santos: Atual, 1993.