Paralelepípedos são sólidos geométricos tridimensionais que pertencem ao conjunto dos prismas. Os prismas são poliedros que possuem duas bases poligonais e paralelogramos como faces laterais. Prismas quadrangulares são aqueles que possuem quadriláteros como bases. Se o prisma quadrangular possui paralelogramos como bases, ele recebe o nome de paralelepípedo.
Exemplos de prismas quadrangulares que possuem
paralelogramos como bases
Classificação dos paralelepípedos
Os paralelepípedos são classificados com relação aos ângulos em sua base e em suas faces laterais:
-
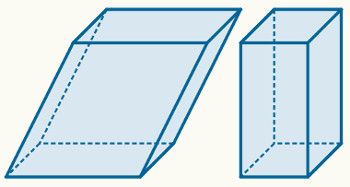
Um prisma reto que possui bases retangulares é um paralelepípedo retângulo. Lembre-se de que retângulos são paralelogramos que possuem todos os ângulos internos retos. Esses paralelepípedos também são chamados de blocos retangulares ou ortoedros.

Exemplo de paralelepípedo que possui retângulos nas bases
Observe que todas as faces de um paralelepípedo retângulo são retângulos, assim, qualquer ângulo encontrado entre duas arestas é reto.
-
Um paralelepípedo que não é retangular é oblíquo. Esse tipo de paralelepípedo não possui todos os ângulos entre duas arestas retos. Observe um exemplo na imagem a seguir:

-
Um paralelepípedo retangular em que todas as faces são quadrados é chamado de cubo, também conhecido como hexaedro regular.
Propriedades das faces e arestas de um paralelepípedo
-
As bases de um paralelepípedo são congruentes e os planos que as contêm são paralelos;
Não pare agora... Tem mais depois da publicidade ;) -
Faces laterais opostas de um paralelepípedo são congruentes e os planos que as contêm são paralelos;
-
As arestas opostas de um paralelepípedo são congruentes e paralelas. Uma aresta de um paralelepípedo é oposta a outras três arestas, como mostra a imagem a seguir.
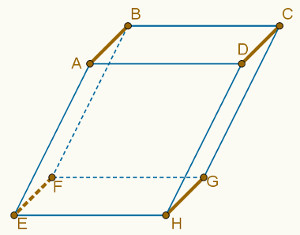
As arestas EF, HG e DC são opostas à aresta AB. A partir dessa propriedade, podemos concluir que essas quatro arestas são, duas a duas, paralelas entre si.
Diagonal do paralelepípedo
Seja a figura a seguir um paralelepípedo e AG uma de suas diagonais. Considere os comprimentos a, b e c, dados na figura como comprimento, largura e altura do prisma.

Nessas condições, a diagonal do paralelepípedo é calculada pela seguinte expressão:
d = √(a2 + b2 + c2)
Se esse prisma for um cubo, todas as suas arestas terão medidas iguais. Seja essa medida x, a diagonal do cubo pode ser calculada por:
d = √(a2 + b2 + c2)
d = √(x2 + x2 + x2)
d = √(3x2)
d = x√3
Exemplo:
Calcule a medida da diagonal de um paralelepípedo que possui 15 m de comprimento, 3 m de largura e 10 m de altura.
Solução:
d = √(a2 + b2 + c2)
d = √(152 + 32 + 102)
d = √(225 + 9 + 100)
d = √(334)
d = 18,27 m, aproximadamente.