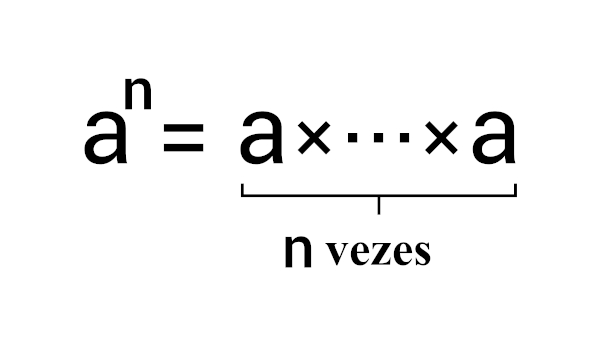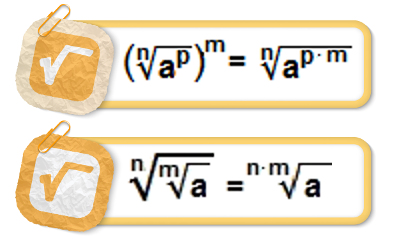A radiciação é a operação matemática inversa da potenciação, assim como a divisão é a operação inversa da multiplicação. Essa operação é representada pelo símbolo √, conhecido como radical, e a raiz de um número é representada por \(\sqrt[n]{a}\ =\ b\). Assim, podemos calcular a raiz enésima de um número utilizando o seguinte raciocínio: a raiz enésima de a é o número que elevado a n é igual a a. Além disso, a radiciação possui propriedades importantes que auxiliam na resolução de problemas envolvendo-a.
Leia também: Potenciação e radiciação de frações
Tópicos deste artigo
- 1 - Videoaula sobre radiciação
- 2 - Como representar a radiciação?
- 3 - Radiciação x potenciação
- 4 - Propriedades da radiciação
- → A raiz enésima de a elevado a n é igual ao próprio a
- → A raiz do produto é igual ao produto das raízes
- → A raiz do quociente é igual ao quociente das raízes
- → Multiplicação e divisão do índice com o expoente
- → Raiz de uma raiz
- → Potência de uma raiz
- → Transformação de uma radiciação em uma potenciação
- 5 - Simplificação de radicais
- 6 - Operações com radicais
- 7 - Exercícios resolvidos sobre radiciação
Videoaula sobre radiciação
Como representar a radiciação?
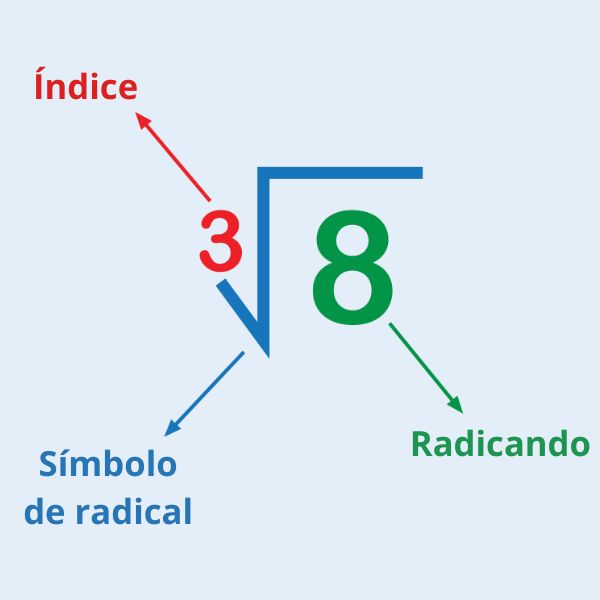
Para representar uma operação de radiciação, utilizamos o símbolo √, conhecido como radical. Então, a raiz de um número é representada por:
\(\sqrt[n]{a}\ =\ b\)
Essa sentença é lida como “raiz enésima de a é igual a b”. Cada um dos elementos recebe nome específico. São eles:
-
√: radical.
-
n: índice.
-
a: radicando.
-
b: raiz.
Observação: Quando o índice é igual a 2, não é necessário que o algarismo 2 conste. Ou seja:
\(\sqrt[2]{a}=\sqrt a\)
Radiciação x potenciação
A radiciação e a potenciação são conhecidas como operações inversas. Assim, para calcular a radiciação, é fundamental saber resolver potenciações. Quando representamos a raiz enésima de a, encontramos como resposta o número b. Para que b seja raiz n de a, temos que:
\(\sqrt[n]{a}=b\rightarrow b^n=a\)
Logo, estamos procurando qual é o número b que elevado ao índice n é igual ao radicando a.
Exemplo 1:
\(\sqrt[2]{25}=5\rightarrow5^2=25\)
Exemplo 2:
\(\sqrt[3]{8}=2\rightarrow2^3=8\)
Exemplo 3:
\(\sqrt[5]{1024}=4\rightarrow4^5=1024\)
Propriedades da radiciação
As propriedades das operações matemáticas são ferramentas que auxiliam na resolução e na simplificação de problemas envolvendo uma operação, e com a radiciação não é diferente. É útil, portanto, dominar algumas propriedades da radiciação.
→ A raiz enésima de a elevado a n é igual ao próprio a
Se queremos calcular a raiz enésima de um número a elevado a n, ou seja, quando o expoente do número é igual ao índice da raiz, a raiz é o próprio número a.
\(\sqrt[n]{a^n}=a\)
→ A raiz do produto é igual ao produto das raízes
Quando o radicando é a multiplicação entre dois números, a raiz do produto é igual ao produto das raízes.
\(\sqrt[n]{a\cdot b}=\sqrt[n]{a}\cdot\sqrt[n]{b}\)
→ A raiz do quociente é igual ao quociente das raízes
Essa propriedade é equivalente à anterior, porém para o caso de divisão. Quando há uma divisão entre dois números no radicando, a raiz do quociente é igual ao quociente das raízes.
\(\sqrt[n]{a∶b}=\sqrt[n]{a}∶\sqrt[n]{b}\)
Além disso, essa propriedade é válida para frações, já que a fração é uma divisão.
\(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\)
→ Multiplicação e divisão do índice com o expoente
Podemos multiplicar ou dividir o radical e o expoente do radicando por um mesmo número.
\(\sqrt[n]{a^m}=\sqrt[n\cdot b]{a^{m\cdot b}}\)
\(\sqrt[n]{a^m}=\sqrt[n:b]{a^{m:b}}\)
→ Raiz de uma raiz
Para resolver a raiz de uma raiz, podemos multiplicar os índices dessas raízes.
\(\sqrt[n]{\sqrt[m]{a}}=\sqrt[n\cdot m]{a}\)
→ Potência de uma raiz
Quando há uma potenciação com a raiz, temos que:
\(\left(\sqrt[n]{a}\right)^b=\sqrt[n]{a^b}\)
→ Transformação de uma radiciação em uma potenciação
Podemos reescrever a radiciação de um número como uma potenciação.
\(\sqrt[n]{a^m}=a^\frac{m}{n}\)
Simplificação de radicais
Quando a raiz não é um número exato, é possível simplificar o radical, ou seja, escrever o radical da forma mais simples possível. Para fazer a simplificação, é necessário fatorar esse número e utilizar as propriedades da radiciação apresentadas anteriormente para representar a radiciação da forma mais simples possível.
Exemplo:
Simplifique \(\sqrt{392}\):
Resolução:
Primeiramente, é necessário realizar a fatoração de 392:

Como queremos calcular a raiz quadrada, agruparemos, quando possível, os números como potência de 2:
392 = \(2^2\cdot2\cdot7^2\)
Assim, temos que:
\(\sqrt{392}=\sqrt{2^2\cdot2\cdot7^2}\)
Utilizando as propriedades da radiciação, sabemos que a raiz do produto é igual ao produto das raízes:
\(\sqrt{392}=\sqrt{2^2}\cdot\sqrt2\cdot\sqrt{7^2}\)
Vale ressaltar que quando o índice não aparece, o seu valor é 2. E quando o índice e o expoente do radicando são os mesmos, a raiz é igual ao radicando. Ou seja:
\(\sqrt{392}=2\cdot\sqrt2\cdot7\)
Então, temos que:
\(\sqrt{392}=14\sqrt2\)
Logo, \(14\sqrt2\) é a forma simplificada da \(\sqrt{392}\).
Operações com radicais
→ Adição e subtração
Quando o radical é o mesmo, para somar ou subtrair a raiz, conservamos o radical e somamos os coeficientes.
Exemplo:
\(4\sqrt2+3\sqrt2=7\sqrt2\)
Quando o radical é diferente, não é possível realizar a operação. Dessa forma, é necessário obter um valor aproximado ou exato para a raiz antes de fazer o cálculo.
Exemplo:
\(5\sqrt3-2\sqrt2\)
\(5\cdot1,7-2\cdot1,4\)
\(8,5-2,8\)
\(5,7\)
→ Multiplicação e divisão
Quando o índice é o mesmo, podemos realizar a multiplicação ou a divisão e conservar o radical.
Exemplo:
\(\sqrt[3]{5}\cdot\sqrt[3]{2}=\sqrt[3]{2\cdot5}=\sqrt[3]{10}\)
Quando o índice é diferente, de início igualamos os índices e depois realizamos a multiplicação/divisão e conservamos o radical.
Exemplo:
\(\sqrt[3]{16}∶\sqrt[2]{2}\)
Para igualar os índices, temos que:
\(\sqrt[3\cdot2]{{16}^2\ }:\sqrt[2\cdot3]{2^3}\)
\(\sqrt[6]{{16}^2∶2^3}\)
\(\sqrt[6]{256∶8}\)
\(\sqrt[6]{32}\)
Exercícios resolvidos sobre radiciação
Questão 1
(Fauel) O número \(\sqrt[3]{2160}\) pode ser escrito na forma simplificada. Assinale a alternativa que apresenta o número simplificado.
A) 50
B) \( 6\sqrt[3]{10}\)
C) \( 10\sqrt[3]{6}\)
D) 720
Resolução:
Alternativa B
Fazendo a fatoração:

Como queremos a raiz cúbica, agruparemos de 3 em 3:
2160 = \(2^3\cdot2\cdot3^3\cdot5\)
Logo:
\(\sqrt[3]{2160}=\sqrt[3]{2^3\cdot2\cdot3^3\cdot5}\)
\(\sqrt[3]{2160}=2\cdot3\sqrt[3]{2\cdot5}\)
\(\sqrt[3]{2160}=6\sqrt[3]{10}\)
Questão 2
Qual é a raiz cúbica de 4.096?
A) 26
B) 24
C) 16
D) 14
Resolução:
Alternativa C
Para encontrar a raiz cúbica de 4.096, devemos fatorar esse número:

Como nós queremos a raiz cúbica, agruparemos de 3 em 3. Assim, obtemos 4096 = \(2^3\cdot2^3\cdot2^3\cdot2^3\).
Portanto:
\(\sqrt[3]{4096}=\sqrt[3]{2^3\cdot2^3\cdot2^3\cdot2^3}\)
\(\sqrt[3]{4096}=2\cdot2\cdot2\cdot2\)
\(\sqrt[3]{4096}=16\)