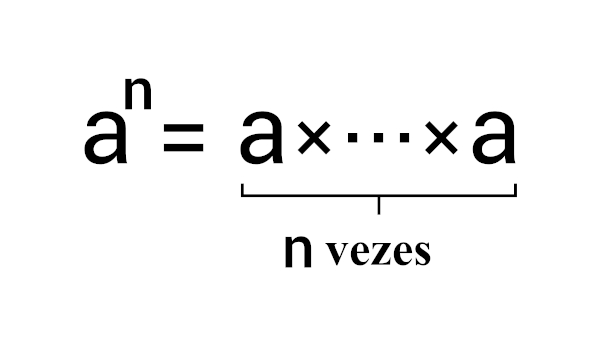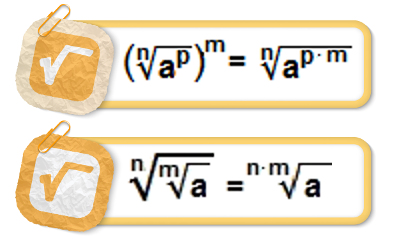Você se recorda de uma operação matemática chamada radiciação? Tenho certeza que sim! Mas caso você tenha se esquecido de algum detalhe, vamos recordá-la rapidamente.
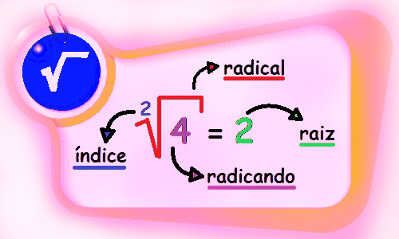
Termos importantes da radiciação
Quando estamos trabalhando com a radiciação, existem algumas propriedades que podem nos auxiliar em diversas situações. Vamos verificar como funciona cada uma delas:
1ª propriedade: ![]()
Se o radical possuir índice igual ao expoente do radicando, a raiz será igual à base do radicando.
Podemos afirmar que essa propriedade será válida sempre que n for um número natural e a for um número real não negativo. Vejamos alguns exemplos da aplicação dessa propriedade:
![]()
Mas nós podemos considerar ainda outra situação em que essa situação é válida. Quando houver um radicando a negativo (a < 0) e n for ímpar, a propriedade também será válida.
![]()
2ª propriedade: ![]()
A raiz não sofre alteração se multiplicarmos ou dividirmos o índice do radical e o expoente do radicando por um mesmo valor.
A segunda propriedade é válida desde que n, p e q sejam números naturais maiores do que 1 e que q seja divisor de n e m. Vejamos alguns exemplos da aplicação dessa propriedade:
![]()
3ª propriedade: ![]()
O produto de radicais de mesmo índice é igual ao produto de radicandos.
Essa propriedade é válida desde que n seja um número natural maior do que 1 e a e b sejam números reais. Se a e b forem maiores ou iguais a zero, é necessário que n seja par. Vejamos alguns exemplos da aplicação dessa propriedade:
![]()
4ª propriedade: ![]()
O quociente de radicais de mesmo índice é igual ao quociente de radicandos.
A quarta propriedade é válida desde que n seja maior do que 1. Além disso, a e b devem ser reais, de forma que a seja maior do que zero, e b, maior do que 1. Vejamos alguns exemplos da aplicação dessa propriedade:
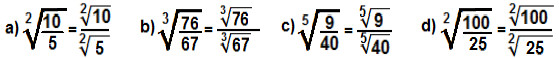
Aproveite para conferir nossa videoaula sobre o assunto: