A função raiz (também chamada de função com radical ou função irracional) é uma função em que a variável aparece no radicando. O exemplo mais simples desse tipo de função é \(f(x)=\sqrt{x}\), que associa cada número real positivo x à sua raiz quadrada \(\sqrt{x}\).
Leia também: Função logarítmica — a função cuja lei de formação é f(x) = logₐx
Tópicos deste artigo
- 1 - Resumo sobre função raiz
- 2 - O que é função raiz?
- 3 - Como a função raiz é calculada?
- 4 - Gráfico da função raiz
- 5 - Exercícios resolvidos sobre função raiz
Resumo sobre função raiz
-
A função raiz é uma função em que a variável aparece no radicando.
-
Geralmente, a função raiz é descrita como uma função na seguinte forma
\(f(x)=\sqrt[n]{p(x)}\)
-
As funções \(\sqrt{x}\) e \(\sqrt[3]{x}\) são exemplos desse tipo de função.
-
Para determinar o domínio de uma função com raiz, é necessário verificar o índice e o logaritmando.
-
Para calcular o valor de uma função para determinado x, basta substituir na lei da função.
O que é função raiz?
Também chamada de função com radical ou função irracional, a função raiz é a função que possui, em sua lei de formação, a variável no radicando. Neste texto, vamos considerar a função raiz como toda função f que apresenta o seguinte formato:
\(f(x)=\sqrt[n]{p(x)}\)
-
n → número natural não nulo.
-
p(x) → polinômio.
Vejamos alguns exemplos desse tipo de função:
\(f(x)=\sqrt{x}\)
\(g(x)=\sqrt[3]{x}\)
\(h(x)=\sqrt{x-2}\)
Importante: o nome função irracional não significa que uma função desse tipo apresenta apenas números irracionais no domínio ou na imagem. Na função \(f(x)=\sqrt{x}\), por exemplo, \(f(4)=\sqrt{4}=2 \) e tanto 2 quanto 4 são números racionais.
O domínio de uma função raiz depende do índice n e do radicando que aparecem em sua lei de formação:
-
Se o índice n é um número par, então a função está definida para todos os números reais em que o logaritmando é maior ou igual a zero.
Exemplo:
Qual o domínio da função \(f(x)=\sqrt{x-2}\)?
Resolução:
Como n = 2 é par, essa função está definida para todos os reais x tais que
\(x - 2 ≥ 0\)
Ou seja,
\(x ≥ 2\)
Logo, \(D(f)=\{x∈R\ |\ x≥2\}\).
-
Se o índice n é um número ímpar, então a função está definida para todos os números reais.
Exemplo:
Qual o domínio da função \(g(x)=\sqrt[3]{x+1}\)?
Resolução:
Como n = 3 é ímpar, essa função está definida para todos os reais x. Logo,
\(D(g)=\mathbb{R}\)
Como a função raiz é calculada?
Para calcular o valor de uma função raiz para determinado x, basta substituir na lei da função.
Exemplo:
Calcule \(f(5)\) e \(f(7)\) para \(f(x)=\sqrt{x-1}\).
Resolução:
Note que \(D(f)=\{x∈R\ |\ x≥1\}\). Assim, 5 e 7 pertencem ao domínio dessa função. Portanto,
\(f(5)=\sqrt{5-1}=\sqrt4\)
\(f(5)=2\)
\(f(7)=\sqrt{7-1}\)
\(f(7)=\sqrt6\)
Gráfico da função raiz
Vamos analisar os gráficos das funções \(f(x)=\sqrt{x}\) e \(g(x)=\sqrt[3]{x}\).
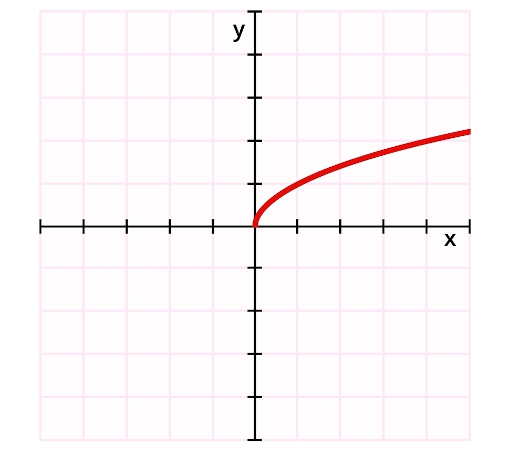
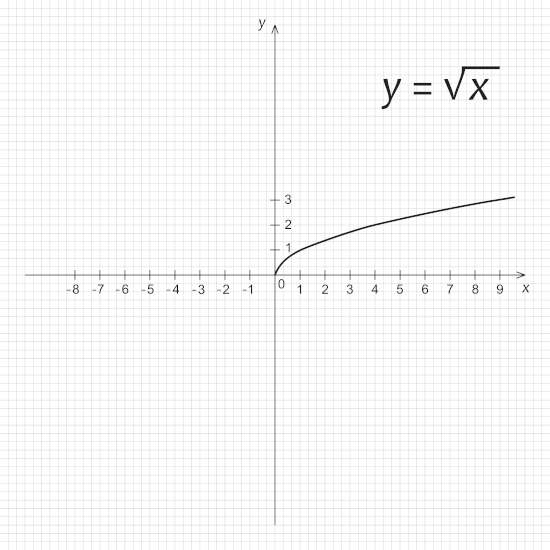
→ Gráfico da função raiz \(\mathbf{f(x)=\sqrt{x}}\)
Note que o domínio da função f é o conjunto dos números reais positivos e que a imagem assume apenas valores positivos. Assim, o gráfico de f está no primeiro quadrante. Além disso, f é uma função crescente, pois quanto maior o valor de x, maior o valor de x.
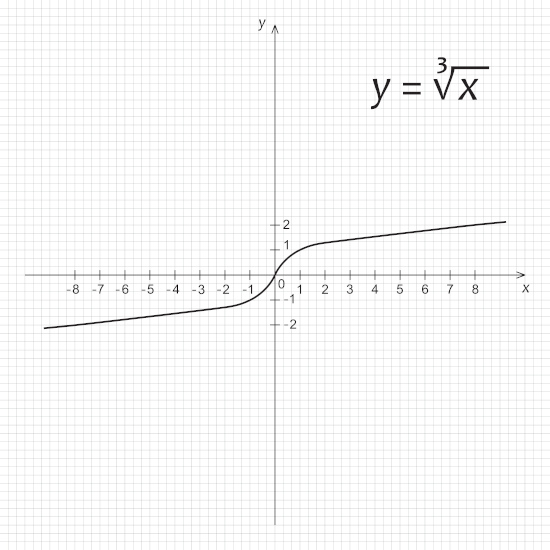
→ Gráfico de uma função raiz \(\mathbf{g(x)=\sqrt[3]{x}}\)
Como o domínio da função f é o conjunto dos números reais, devemos analisar o que acontece para os valores positivos e negativos:
-
Quando x é positivo, o valor de \(\sqrt[3]{x}\) também é positivo. Além disso, para \(x>0\), a função é crescente.
-
Quando x é negativo, o valor de \(\sqrt[3]{x}\) também é negativo. Além disso, para \(x<0\), a função é decrescente.
Acesse também: Como construir o gráfico de uma função?
Exercícios resolvidos sobre função raiz
Questão 1
O domínio da função real \(f(x)=2\sqrt{3x+7}\) é
A) \( (-∞;3]\)
B) \( (-∞;10]\)
C) \( [-7/3;+∞)\)
D) \( [0;+∞)\)
E) \( [\frac{7}{3};+∞)\)
Resolução:
Alternativa C.
Como o índice do termo \(\sqrt{3x+7}\) é par, o domínio dessa função é determinado pelo logaritmando, que deve ser positivo. Assim,
\(3x+7≥0\)
\(3x≥-7\)
\(x≥-\frac{7}3\)
Questão 2
Considere a função \(g(x)=\sqrt[3]{5-2x}\). A diferença entre \(g(-1,5)\) e \(g(2)\) é
A) 0,5.
B) 1,0.
C) 1,5.
D) 3,0.
E) 3,5.
Resolução:
Alternativa B.
Como o índice é ímpar, a função está definida para todos os reais. Assim, podemos calcular \(g(-1,5)\) e \(g(2)\) ao substituir os valores de x na lei da função.
\(g(-1,5)=\sqrt[3]{5-2 · (-1,5)}\)
\(g(-1,5)=\sqrt[3]{5+3}\)
\(g(-1,5)=\sqrt[3]8\)
\(g(-1,5)=2\)
Ainda,
\(g(2)=\sqrt[3]{5-2 · (2)}\)
\(g(2)=\sqrt[3]{5-4}\)
\(g(2)=\sqrt1\)
\(g(2)=1\)
Portanto,
\(g(-1,5)-g(2) = 2 - 1 = 1\)
Fontes
LIMA, Elon L. et al. A Matemática do Ensino Médio. 11. ed. Coleção Professor de Matemática. Rio de Janeiro: SBM, 2016. v.1.
PINTO, Márcia M. F. Fundamentos de Matemática. Belo Horizonte: Editora UFMG, 2011.