A equação reduzida da reta é a que nos permite descrever de forma algébrica o comportamento da reta. Analisando essa equação, é possível obter informações importantes sobre a reta, como o seu comportamento, se ela é crescente ou decrescente, e também o momento em que a reta corta o eixo y.
A equação reduzida da reta é a y = mx + n, em que m e n são números reais. O m é conhecido como coeficiente angular, e, ao analisá-lo, é possível saber mais sobre a inclinação da reta. O n é o coeficiente linear, sendo o valor de y para o ponto em que a reta corta o eixo vertical.
Leia também: Qual é a equação geral da circunferência?
Tópicos deste artigo
- 1 - A equação reduzida da reta
- 2 - Coeficiente angular
- 3 - Coeficiente linear
- 4 - Como calcular a equação reduzida da reta?
- 5 - Representação gráfica da reta com base na equação reduzida
- 6 - Exercícios resolvidos
A equação reduzida da reta
A geometria analítica é a área da matemática que analisa de forma algébrica elementos da geometria, como ponto, reta, circunferência, cônicas, entre outros. Essa representação da reta por meio de uma equação pode ser feita de mais de uma maneira, uma delas é a equação reduzida. A equação reduzida da reta é a expressão:
y = mx + n
m → coeficiente angular
n → coeficiente linear
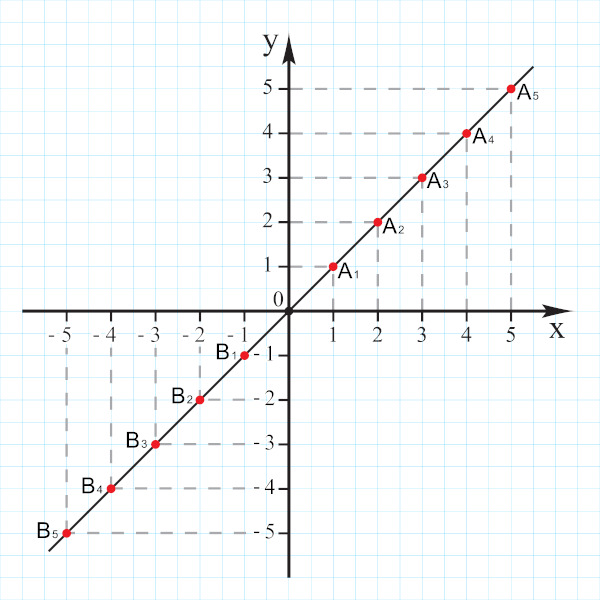
As variáveis x e y são pontos do plano cartesiano (x, y) que pertencem à reta. Já m é o coeficiente angular, que indica a inclinação da reta em relação ao eixo x, e n é o coeficiente linear, que indica o ponto em que o gráfico da reta intercepta o eixo y.
Exemplos:
a) y = 2x – 5
m = 2 e n = -5
b) y = – x + 1
m = -1 e n = 1
c) y = 3x
m = 3 e n = 0
d) y = -4
m = 0 e n = -4
Veja também: O que é um par ordenado?
Coeficiente angular
Para encontrar a equação da reta, precisamos aprender a encontrar o coeficiente angular. O coeficiente angular nos indica muito sobre a reta, pois é com base nele que podemos analisar sua inclinação em relação ao eixo x.
Para encontrar o valor do coeficiente angular conhecendo o ângulo que a reta faz com o eixo x, basta calcular a tangente desse ângulo:
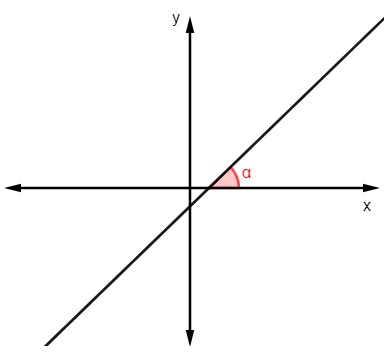
|
m = tgα |
Exemplo:
Encontre o coeficiente angular da reta:
a)
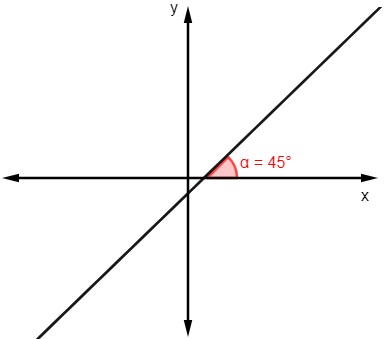
m = tg 45º
m = 1
b)
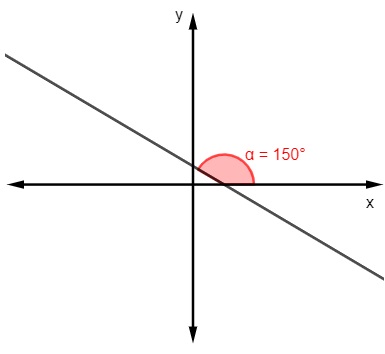
m = tg 150º
m = -√3/3
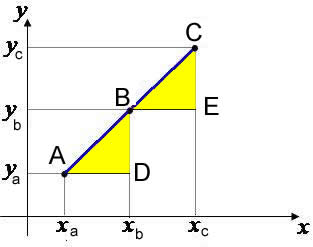
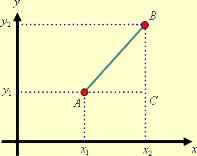
A segunda maneira de encontrar o coeficiente angular de uma reta leva em consideração a outra forma de calcular a tangente. Para aplicar esse método, é necessário conhecer dois pontos pertencentes à reta.
Sabemos que a tangente é a razão entre o cateto oposto e o cateto adjacente do triângulo, sendo assim, para calcular o coeficiente angular, temos que:
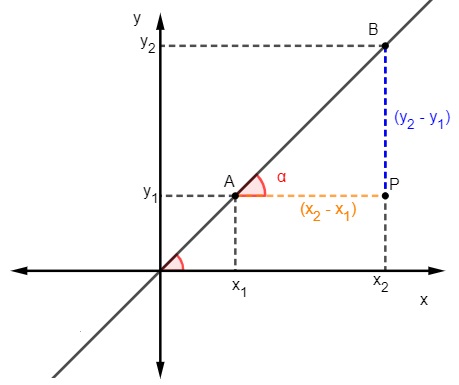
Sabemos que m = tgα, mas a tangente é a razão entre o cateto oposto e o cateto adjacente, então, temos que:
![]()
Exemplo:
Encontre a equação da reta que passa pelos pontos A(2, 3) B(4, 7).
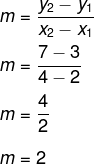
Existem três classificações possíveis para a reta, ela pode ser crescente, constante ou decrescente. Podemos identificar o comportamento da reta de acordo com o valor do seu coeficiente angular.
Quando m > 0, ou seja, quando o coeficiente angular é positivo, a reta será crescente.
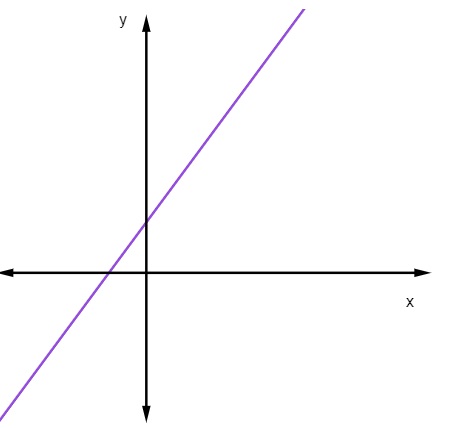
Na reta crescente, à medida que o valor de x aumenta, o valor de y também aumentará.
Quando m = 0, a reta será constante.
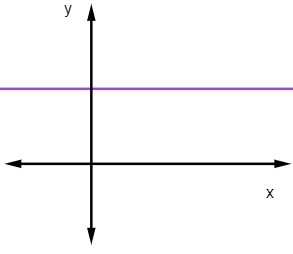
Na reta constante, independentemente do valor de x, o valor de y é sempre o mesmo.
Quando m < 0, ou seja, quando o coeficiente angular é negativo, a reta será decrescente.
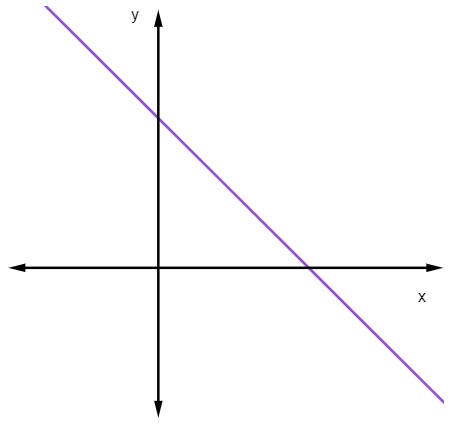
Quando uma reta é decrescente, à medida que o valor de x aumenta, o valor de y diminui.
Leia também: Como calcular a distância entre dois pontos no espaço?
Coeficiente linear
O coeficiente linear n nos indica o ponto em que a reta intercepta o eixo y.
Sabemos que, nesse ponto, x = 0. Como a equação é y = mx + n, temos que:
x = 0
y = m · 0 + n
y = n
O que significa que o ponto em que a reta corta o eixo y é sempre o ponto (0, n).
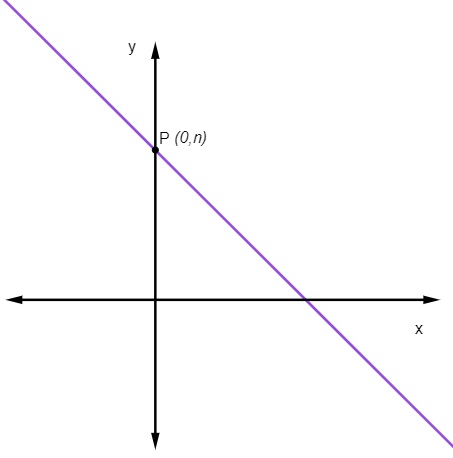
Como calcular a equação reduzida da reta?
Encontrar a equação reduzida da reta é buscar o valor de m e n na equação y = mx + n.
Exemplo:
Encontre a equação da reta que passa pelos pontos A(1, 1) e B (2, 4).
-
1º passo: encontrar o coeficiente angular.
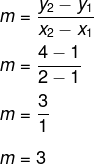
-
2º passo: substituir na equação y = mx + n o valor encontrado para o coeficiente angular.
y = 3x + n
-
3º passo: escolher um dos pontos para substituir na equação e encontrar o valor de n.
A (1, 1)
1 = 3 · 1 + n
1 = 3 + n
1 – 3 = n
-2 = n
n = -2
-
4º passo: escrever a equação reduzida substituindo os valores de m e n encontrados:
y = 3x – 2
Veja também: Qual é a equação geral da reta?
Representação gráfica da reta com base na equação reduzida
Conhecendo a equação, é possível também representar no plano cartesiano a reta, para isso, basta encontrar dois pontos da equação. Um deles é fácil de identificar, que é o ponto em que a reta corta o eixo y, ou seja, o ponto (0, n); já o outro será o ponto (x, 0), em que x é um número real.
Exemplo:
y = 2x + 4
O primeiro ponto é A(0, 4).
Já o segundo será o ponto em que y = 0, ou seja:
0 = 2x + 4
-2x = 4 (-1)
2x = -4
x = -4/2
x = -2
B (-2, 0)
Por fim, basta representar esses pontos no plano cartesiano e traçar a reta que passa por eles.
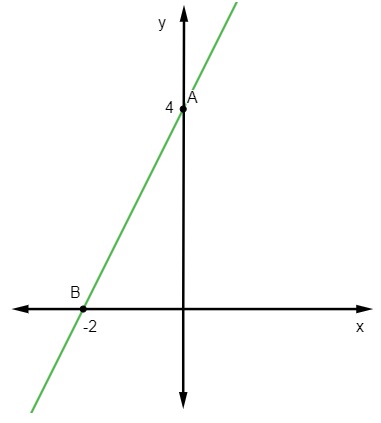
Exercícios resolvidos
Questão 1 – (Udesc) A soma do coeficiente angular com o coeficiente linear da reta que passa pelos pontos A(1, 5) e B(4, 14) é:
A) 4
B) -5
C) 3
D) 2
E) 5
Resolução
Alternativa E
Calculando o valor do coeficiente angular m, temos que:
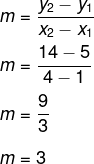
Agora, vamos calcular o coeficiente linear:
y = mx + n
y = 3x + n
Escolhendo o ponto A(1,5):
5 = 3 · 1 + n
5 = 3 + n
5 – 3 = n
2 = n
n = 2
A soma m + n = 3 + 2 = 5
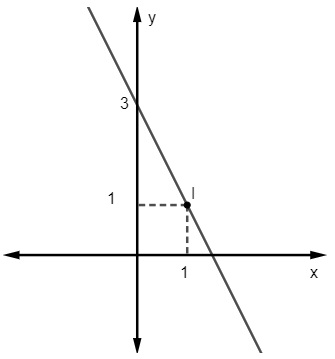
Questão 2 – A equação da reta a seguir é:
A) y = 2x – 3
B) y = x + 1
C) y = – 2x + 3
D) y = 3x – 1
E) y = 2 – 3x
Resolução
Alternativa C
Dada a equação y = mx + n, sabemos que n = 3, pois a reta corta o eixo y no ponto (0, 3). Além disso, outro ponto que pertence à reta é o (1, 1), logo, calcularemos m.
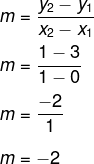
Dessa forma, a equação da reta é y = – 2x + 3.