A equação geral da circunferência é uma equação que descreve a circunferência de forma algébrica. A Geometria Analítica nos possibilita representar objetos geométricos por meio de uma equação, e a circunferência pode ser representada por meio de uma equação conhecida como equação geral da circunferência de centro C (a, b) e raio r, que é a equação x² + y² – 2ax – 2by + a² + b² – r² = 0. Para encontrar a equação de uma circunferência representada no plano cartesiano, é necessário conhecermos as coordenadas do seu centro e do seu raio.
Veja também: Círculo — a região plana que apresenta uma circunferência como limite
Tópicos deste artigo
- 1 - Resumo sobre equação geral da circunferência
- 2 - Qual é a equação geral da circunferência?
- 3 - Como calcular a equação geral da circunferência?
- 4 - Como calcular o centro e o raio da circunferência?
- 5 - Exercícios resolvidos sobre equação geral da circunferência
Resumo sobre equação geral da circunferência
-
A equação geral da circunferência representa de forma algébrica a circunferência.
-
A equação geral da circunferência de centro C (a, b) e raio r é a equação:
\(x²+y² –2ax –2by+a²+b² –r²=0\)
-
Para encontrar a equação geral de uma circunferência, é necessário conhecer o seu centro e o seu raio.
-
Podemos descrever a equação geral da circunferência analisando a sua representação no plano cartesiano.
Qual é a equação geral da circunferência?
Considerando uma circunferência de centro C (a,b) e raio r, a equação geral da circunferência é uma maneira de demonstrar a circunferência de forma algébrica. A equação da geral circunferência é:
\(x² + y² – 2ax – 2by + a² + b² – r² = 0\)
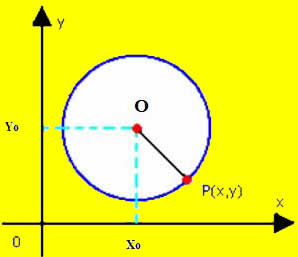
Sabemos que a circunferência é o conjunto de pontos que estão a uma mesma distância do centro C (a,b). Para calcular a distância entre o ponto C e o ponto A (x, y), utilizamos a equação:
\(\sqrt{\left(x-a\right)^2+\left(y-b\right)^2}=dAB\)
A distância entre esses pontos é conhecida como raio da circunferência. Então, temos:
\(\sqrt{\left(x-a\right)^2+\left(y-b\right)^2}=r\)
Elevando os dois lados ao quadrado, podemos eliminar a raiz:
\(\left(x-a\right)^2+\left(y-b\right)^2=r^2\)
Agora, desenvolvendo as potências:
\(x^2-2ax+a^2+y^2-2bx+b^2-r^2=0\)
Por fim, basta mudar a ordem dos termos para encontrar a equação geral da circunferência:
\(x²+y² –2ax –2by+a²+b² – r²=0\)
Como calcular a equação geral da circunferência?
Para encontrar a equação geral da circunferência, conhecendo seu raio e centro, basta substituir os valores de a e b pelos valores das coordenadas do centro da circunferência e o valor de r pelo valor do raio.
-
Exemplo 1
Encontre a equação geral da circunferência com centro (2, -3) e raio igual a 5.
Resolução:
Dados:
\(a=2,\ b=-\ 3\ e\ r=5\)
Então, temos:
\(x²+y² –2ax –2by+a²+b² –r²=0\)
\(x^2+y^2–2⋅2⋅x–2⋅-3⋅y+22+-32–52=0\)
\(x^2+y^2-4x\ +6y+4+9\ –25=0\)
Assim, a equação geral da circunferência é:
\(x^2+y^2-4x\ +6y+\ –12=0\)
-
Exemplo 2
Encontre a equação geral da circunferência:
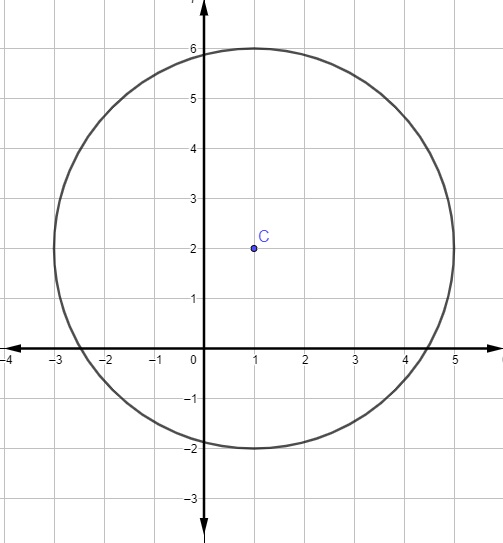
Resolução:
Analisando a imagem, é possível verificar que o centro da circunferência é o ponto C (1,2). Para encontrar o raio, basta notar que a distância do centro até a extremidade da circunferência é de 4 unidades, logo r = 4.
Agora que conhecemos o raio e o centro, basta substituir na equação geral da circunferência:
\(x²+y² –2ax –2by+a²+b² –r²=0\)
\(x^2+y^2–2⋅1⋅x–2⋅2⋅y+12+22–42=0\)
\(x^2+y^2–2x–4y+1+4 –16=0\)
Então, a equação geral da circunferência é:
\(x^2+y^2–2x–4y-11=0\)
Como calcular o centro e o raio da circunferência?
Para calcular o centro e o raio da circunferência, conhecendo a equação geral da circunferência, utilizamos um método conhecido como método da comparação dos termos da circunferência.
-
Exemplo
Qual é o centro da circunferência com a equação geral abaixo?
\(x^2+y^2-10x+14y+10=0\)
Resolução:
Para utilizar o método da comparação, igualaremos as equações:
\(x^2+y^2-10x+14y+10=x^2+y^2-2ax-2by+a^2+b^2-r^2\)
Note então que:
\(-10x=-2ax\)
Então, temos:
\(-10x=-2ax\ \)
\(\frac{-10}{-2}x=ax\)
\(5x=ax\)
\(5=a\)
Portanto, \( a=5\).
Para calcular o valor de b, compararemos o termo:
\(14\ y=-\ 2by\)
\(14y=-2by\)
\(\frac{14}{-2}y=by\)
\(-7y=by\)
\(-7=b\)
\(b=-7\)
Então, o centro da circunferência é o ponto C \( (5,\ -\ 7)\).
Após encontrarmos o centro da circunferência, é possível calcular o seu raio, pois analisando o termo independente da equação, temos:
\(a^2+b^2-r^2=10\)
Substituindo os valores do centro:
\(5^2+\left(-7\right)^2-r^2=10\)
\(25+49-r^2=10\)
\(74-r^2=10\)
\(-r^2=10-74\)
\(-r^2=-64\left(-1\right)\)
\(r^2=64\)
\(r=\sqrt{64}\)
\(r=8\)
Leia também: Equação geral da reta — a maneira algébrica de estudar uma reta no plano cartesiano
Exercícios resolvidos sobre equação geral da circunferência
Questão 1
O raio da circunferência que possui equação geral igual a \(x^2+y^2+4x-10y+13=0\) é igual a:
A) 1
B) 2
C) 3
D) 4
E) 5
Resolução:
Alternativa D
Utilizando o método da comparação, temos:
\(-2ax=4x\ \)
\(ax=\frac{4}{-2}x\)
\(ax=-\ 2x\)
\(a=-2\ \)
Em seguida, calcularemos o valor de b:
\(-\ 2by=-\ 10y\)
\(by=\frac{-10}{-2}y\)
\(by=5y\)
\(b=5\)
Agora, para encontrar o raio, temos:
\(a^2+b^2-r^2=13\)
\(\left(-2\right)^2+5^2-r^2=13\)
\(4+25-r^2=13\)
\(29-r^2=13\)
\(-r^2=13-29\)
\(-r^2=-16\left(-1\right)\)
\(r^2=16\)
\(r=\sqrt{16}\)
\(r=4\ \)
Questão 2
Uma circunferência que possui raio igual a 3 cm e centro igual a C (4, -5) possui equação geral igual a:
A) \(x^2+y^2-8x+10y+32=0\)
B) \( x^2+y^2-8x+10y+9=0\)
C) \( x^2+y^2+4x+5y+9=0\)
D) \(x^2+y^2+8x\ -\ 10y+32=0\)
E) \( x^2+y^2-4x+5y+3=0\)
Resolução:
Alternativa A
Calculando a equação geral da circunferência:
\(a=4,\ b=-\ 5\ e\ r=3\)
\(x^2+y^2-2ax-2ay+a^2+b^2-r^2=0\)
\(x^2+y^2-2\cdot4x-2\cdot\left(-5\right)y+4^2+\left(-5\right)^2-3^2=0\)
\(x^2+y^2-8x+10y+16+25-9=0\)
\(x^2+y^2-8x+10y+32=0\)