Os juros compostos são bastante recorrentes em empréstimos bancários, financiamentos de moradia ou carro e também em investimentos como poupança, entre outros. Na matemática financeira, para trabalhar com os juros compostos, é necessário compreender cada uma das suas variáveis, são elas:
-
o capital, que é o valor inicial;
-
a taxa de juros, que é a porcentagem cobrada de juros ao decorrer do tempo;
-
o tempo, que pode ser contado em dias, meses, bimestres, semestres, anos, ou seja, em qualquer intervalo de tempo;
-
o montante, que é o valor resgatado ao final da transação.
Para calcular os juros compostos, usamos uma fórmula específica com cada um desses elementos. Além deles, existem os juros simples. A diferença entre ambos é que, nos juros simples, os juros serão fixos, cobrados em cima do capital somente, já nos juros compostos, há uma cobrança de juros em cima do valor anterior, do capital mais os juros, ou seja, há juros sobre juros. Isso faz com que os juros compostos resultem em valores maiores que os juros simples ao decorrer do tempo.
Leia também: 3 macetes matemáticos para o Enem
Tópicos deste artigo
- 1 - Fórmula do juros composto
- 2 - Como calcular os juros compostos
- 3 - Diferença entre juros simples e juros compostos
- 4 - Exercícios resolvidos sobre juros compostos
Fórmula do juros composto
A fórmula dos juros compostos é formada por quatro variáveis, são elas: capital, juros, taxa de juros, tempo e montante.
|
M = C (1 + i)t |
M: montante
C: capital
i: taxa de juros
t: tempo
-
Capital (C): é o primeiro valor da negociação; é o valor que pegamos emprestado em um caso de financiamento ou o valor que foi investido primeiro; é o valor inicial que serve como referência para calcular os juros.
-
Montante (M): é o valor final da minha transação. Após um tempo, ao valor do meu capital será adicionado o que chamamos de juros. O valor final, ou seja, a soma do capital com os juros, gera o que conhecemos como montante: M = C + J.
-
Juros (J): muitas vezes confundido com a taxa de juros, os juros são o valor de correção do capital, ou seja, são o valor adquirido a mais, calculado em cima do capital ao decorrer do tempo. Em um empréstimo, por exemplo, juros são o valor pago a mais ao final do prazo; em um investimento, são o rendimento adquirido em cima do capital. Eles são calculados pela diferença entre o montante e o capital, ou seja: J = M – C.
-
Tempo (t): é o prazo em que o capital ficará na transação. Ele pode ser dado em qualquer unidade de tempo, ou seja, em dias, meses, bimestres, semestres, anual. É importante que o tempo e a taxa de juros estejam com a mesma unidade de medida para realizar-se o cálculo.
-
Taxa de juros (i): é a porcentagem cobrada a cada intervalo de tempo.
Veja também: O que é índice percentual?
Como calcular os juros compostos
Para calcular os juros compostos, ou qualquer outra variável envolvendo-os, basta substituir os valores conhecidos na fórmula, para isso, é necessário o domínio da resolução de equações.
Exemplo 1:
Um capital de R$ 4000 foi aplicado a juros compostos, com taxa de 10% a.a. Qual será o montante e os juros gerados após 3 anos?
Dados:
C = 4000
t = 3 anos
i = 10% a.a.
Vamos representar 10% em sua forma decimal = 0,1.
Temos que:
M = C (1 + i) t
M = 4.000 (1 + 0,1)³
Após a substituição, vamos resolver a equação:
M = 4000 (1,1)³
M = 4000 · 1331
M = 5324
Para encontrar os juros, basta calcular a diferença J = M – C:
J = M – C = 5324 – 4000 = 1324
Então, temos que:
M = R$ 5324
J = R$ 1324
Exemplo 2:
Durante quanto tempo um capital deve ser investido a uma taxa de 5% a.a para que ele dobre o seu valor? (Use log 1,05 = 0,2 e log 2 = 0,3)
Se o montante será o dobro do capital, então, temos que:
M = 2C
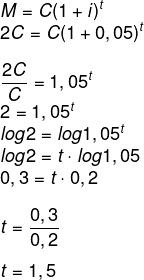
1 ano e meio, ou seja, 1 ano e 6 meses.
Diferença entre juros simples e juros compostos
A diferença entre os juros simples e os juros compostos inicia-se ao analisarmos matematicamente o comportamento de cada um deles. Acontece que as fórmulas de cálculo são diferentes, os juros simples são calculados pela fórmula:
J = C · i · t
Nesse caso, ao trabalhar com juros simples, o valor somado a cada ciclo é sempre o mesmo, por exemplo:
Se em um investimento de R$ 1000 os juros forem de 10% ao mês, então, a cada mês, no regime de juros simples, serão acrescentados R$ 100, assim, no decorrer de 5 meses, haveria um aumento de R$ 500, então, o montante seria de R$ 1500.
Nos juros compostos, o comportamento é bem diferente. Para valores e intervalos de tempo maiores, a diferença torna-se muito grande. Utilizando-se do mesmo valor, R$ 1000, a juros de 10% ao mês, no primeiro mês, o acréscimo seria o mesmo que nos juros simples, ou seja, R$ 100, porém, a partir do segundo mês, esses juros serão calculados em cima do valor atual e não do inicial. Como agora temos R$ 1100, os juros serão de 10% desse valor, R$ 110, resultando em R$ 1210 no segundo mês.
No terceiro mês, calcula-se mais uma vez 10% do valor atual (R$ 1210), que é igual a R$ 121, gerando um total de R$ 1232, repetindo-se esse processo se esse capital ficar o mesmo tempo que o outro, ou seja, 5 meses. Se for o caso, ele vai gerar um montante de R$ 1610,51. A diferença nesse prazo foi de R$ 110,51 entre os juros simples e os juros compostos, mas, ao realizar esse mesmo cálculo para valores e tempo maiores (por exemplo, em um financiamento de imóvel durante 30 anos), a diferença é muito grande.
Note que os juros compostos têm o tempo como expoente, comportando-se como uma função exponencial, o que não acontece nos juros simples, que se comportam de forma linear, ou seja, o gráfico é uma reta.
Acesse também: Funções no Enem: como esse tema é cobrado?
Exercícios resolvidos sobre juros compostos
Questão 1 – Os juros adquiridos ao investir-se um capital de R$ 20.000 a juros compostos, de 3% a.a., durante um período de 24 meses, serão de:
A) R$ 22.315
B) R$ 21.218
C) R$ 1218
D) R$ 2414
E) R$ 1310
Resolução
Alternativa C
Dados: C = 20.000
i = 3% a.a.
t = 24 meses = 2 anos (note que a taxa está em anos)
M = C (1 + i)t
M = 20.000 (1 + 0,03)2
M = 20.000 (1,03)²
M = 20.000 · 1,0609
M = 21.218
J = M – C = 21.218 – 20.000 = 1218
Questão 2 – (Fauel 2019) Um pequeno investidor decide realizar uma aplicação no Tesouro Direto, um fundo de investimento muito pouco arriscado, porém que rende mais que a poupança tradicional. Considerando-se que tal investimento rende aproximadamente 7% ao ano no regime de juros composto, quanto uma aplicação de R$ 100 renderia ao final de dois anos?
A) R$ 13,85
B) R$ 14,00
C) R$ 14,49
D) R$ 15,23
Resolução
Alternativa C
C = 100
t = 2 anos
i = 7%
M = C (1 + i)t
M = 100 (1 + 0,07)²
M = 100 (1,07)²
M = 100*1,1449
M = 114,49
Calculando os juros, temos que:
J = M – C
J = 114,49 – 100 = 14,49










