O chamariz das vendas nos mercados são as vendas “sem juros”, nas quais o cliente é levado a pensar que a mercadoria que está sendo paga não possui juros no parcelamento de sua compra. Contudo, nem sempre isso é verdade: trata-se dos famosos juros embutidos. Podemos descobrir qual seria o valor real do produto comprado caso ele fosse adquirido à vista. Para tanto, necessitaremos do auxílio da matemática financeira e seus conceitos.
Podemos determinar o valor atual de uma mercadoria, ou o valor real, através de uma expressão matemática, que envolve a quantidade de parcelas com os juros aplicados.
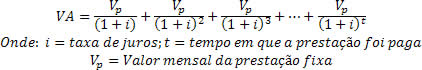
Note que a expressão foi definida com um valor fixo para a prestação (Vp – Valor da prestação), portanto com esses dados podemos definir qual seria o valor atual do produto se este fosse comprado à vista. Veja um exemplo para compreender a aplicação dessa expressão. OBS.: o valor da prestação pode ser diferente a cada mês.
“O anúncio de uma loja de eletrodoméstico contém a seguinte informação: Compre agora sua máquina de lavar roupas, em até 5x sem juros no cartão de crédito, com a pequena parcela de 600 reais.”
Sabemos que quase toda compra no cartão de crédito possui um valor adicional, que já foi incluso na prestação, por isso pensamos que de fato não estamos pagando nenhum juro. Contudo, se considerarmos que o juro embutido foi de 2% ao mês, pode-se determinar o Valor Atual desse eletrodoméstico, ou seja, determinar qual seria o valor dele sem os juros embutidos em cada parcela.
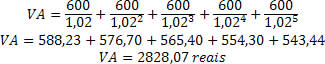
Note que o eletrodoméstico é anunciado a um valor de três mil reais. No entanto, no cálculo do valor atual, obtemos uma diferença de quase duzentos reais: estes são os juros embutidos nas parcelas.
Portanto, a Estimativa do Valor Atual determina qual é o valor de algo com a ausência dos juros aplicados. Note que se somarmos apenas os numeradores, obteremos o valor pago das prestações nos 5 meses, os três mil reais. Contudo, cada mês foi dividido pela taxa de juros acumulada, de forma que sejam retirados os juros sobre aquela parcela, obtendo assim um valor sem os juros embutidos.




