A reta numérica é uma reta numerada e ordenada onde cada um de seus pontos representa um único número real. Assim, não há ponto que represente dois números ou número relacionado a dois pontos.
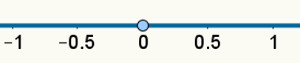
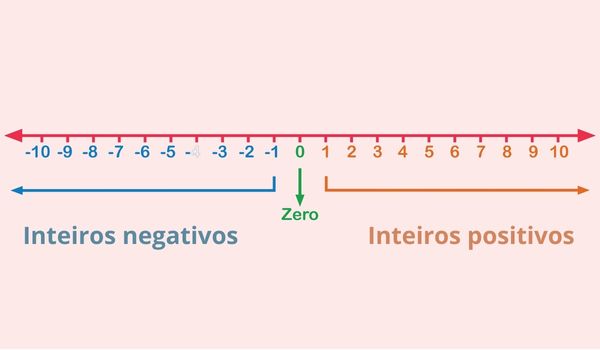
Exemplo de reta numérica contendo alguns números inteiros
A construção da reta numérica
Existem três etapas básicas na construção de retas numéricas. Observe:
1 – Dada uma reta qualquer, escolha um de seus pontos para ser a origem. A esse ponto será atribuído o número real 0 (zero).
2 – Escolha um sentido crescente para essa reta. Usualmente as retas numéricas são representadas na horizontal ou na vertical. O sentido crescente, nesses casos, é colocado da esquerda para a direita nas retas horizontais e de baixo para cima nas retas verticais.
Tomando como exemplo uma reta horizontal, onde já foi escolhido o ponto chamado origem, os números à direita desse ponto serão positivos e quanto maior a distância entre o ponto e a origem, maior será o número real que o representa.
3 – Escolha uma unidade de medida (centímetros, por exemplo) e marque todos os pontos que forem possíveis na reta. Isso porque é impossível marcar todos os pontos, pois o conjunto dos números reais é infinto. Cada número inteiro deve ser marcado à distância de 1 unidade de medida do seu antecessor. Fica óbvio que os números decimais estão entre os respectivos inteiros. Os números irracionais resultantes de raízes não exatas podem ser marcados usando processos geométricos.
Essas três etapas garantem que a reta conterá todos os números reais representados pelos seus pontos.
Formalização
Um segmento de reta é uma parte de uma reta que possui início e fim. Logo, é possível medir a distância entre os pontos inicial e final desse segmento.
Essa distância entre dois pontos sempre é representada por um número real diferente para diferentes distâncias.
Assim, tomamos a distância entre todos os pontos da reta numérica e a origem e as relacionamos de maneira biunívoca aos números reais. Isso significa que existe uma espécie de função bijetora que relaciona cada ponto da reta ao número real que representa a distância entre esse ponto e a origem. Assim, cada ponto da reta representa um único número real e não existe um número real que não seja representado na reta.
Observe o exemplo abaixo do ponto + 5, representado na reta numérica.

Exemplo de representação do ponto + 5 em uma reta numérica
Retas numéricas na realidade
Os dois objetos mais conhecidos que podem representar uma parte da reta numérica são a régua e o escalímetro: objetos usados para medir distâncias no espaço; ambos graduados com alguns números reais. A régua é usada para medir distâncias em centímetros e o escalímetro, para converter medidas em outras unidades também muito usuais, como as polegadas, por exemplo.