O teorema da bissetriz interna demonstra que quando traçamos a bissetriz de um ângulo interno do triângulo, ela divide o lado oposto a esse ângulo em segmentos de retas que são proporcionais aos lados adjacentes a esse ângulo. Com o teorema da bissetriz interna podemos determinar qual é a medida dos lados do triângulo ou mesmo dos segmentos divididos pelo ponto de encontro da bissetriz, utilizando a proporção.
Saiba mais: Condição de existência de um triângulo — a verificação da existência dessa figura
Tópicos deste artigo
- 1 - Resumo sobre teorema da bissetriz interna
- 2 - Videoaula sobre teorema da bissetriz interna
- 3 - O que diz o teorema da bissetriz interna?
- 4 - Demonstração do teorema da bissetriz interna
- 5 - Exercícios resolvidos sobre teorema da bissetriz interna
Resumo sobre teorema da bissetriz interna
-
A bissetriz é uma semirreta que divide um ângulo ao meio.
-
O teorema da bissetriz interna demonstra uma relação de proporção entre os lados adjacentes ao ângulo e os segmentos de reta do lado oposto ao ângulo.
-
Utilizamos o teorema da bissetriz interna para encontrar medidas desconhecidas em triângulos.
Videoaula sobre teorema da bissetriz interna
O que diz o teorema da bissetriz interna?
A bissetriz de um ângulo é uma semirreta que divide um ângulo em dois ângulos congruentes. O teorema da bissetriz interna nos mostra que ao traçar a bissetriz de um ângulo interno de um triângulo, ela encontra o lado oposto em um ponto P, dividindo-o em dois segmentos de reta. Ou seja, os segmentos divididos pela bissetriz de um ângulo interno do triângulo são proporcionais aos lados adjacentes do ângulo.
Os segmentos de reta formados pelo ponto de encontro da bissetriz de um ângulo com o lado oposto a esse ângulo possuem uma proporção com os lados que são adjacentes a esse ângulo. Veja no triângulo a seguir:
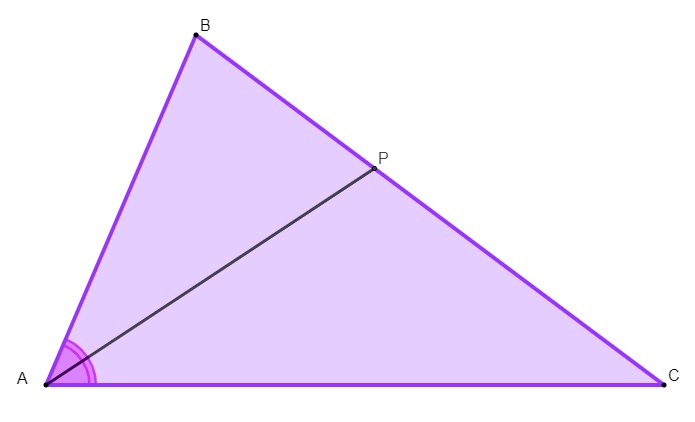
A bissetriz do ângulo A divide o lado oposto nos segmentos \(\overline{BP}\) e \(\overline{CP}\). O teorema da bissetriz interna demonstra que:
\(\frac{\overline{AB}}{\overline{BP}}=\frac{\overline{AC}}{\overline{CP}}\)
-
Exemplo
Dado o triângulo a seguir, sabendo que AP é a sua bissetriz, o valor de x é:
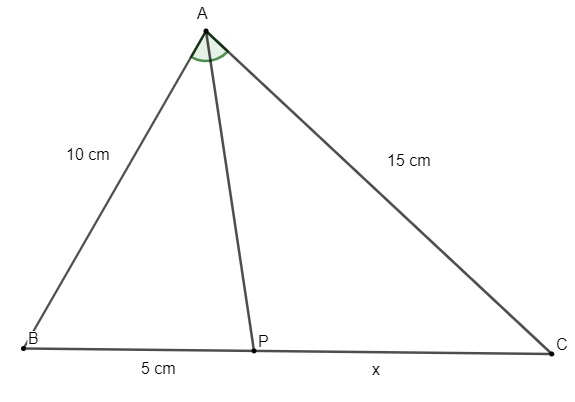
Resolução:
Para encontrar o valor de x, aplicaremos o teorema da bissetriz interna.
\(\frac{10}{5}=\frac{15}{x}\)
Multiplicando cruzado, temos que:
\(10x=15\cdot5\)
\(10x=75\)
\(x=\frac{75}{10}\)
\(x=7,5\ cm\)
Portanto, o lado CP mede 7,5 centímetros.
Demonstração do teorema da bissetriz interna
Conhecemos como demonstração de um teorema a prova de que ele é verdade. Para demonstrar o teorema da bissetriz interna, vamos seguir alguns passos.
No triângulo ABC com a bissetriz AP, traçaremos o prolongamento do lado AB até ele se encontrar com o segmento CD, que será delineado de forma paralela à bissetriz AP.
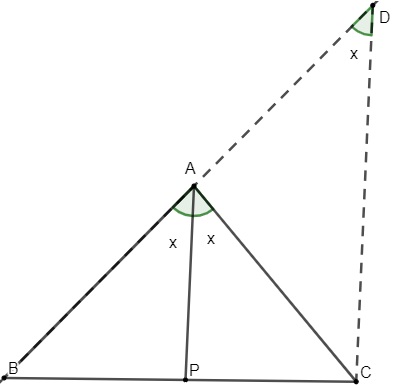
Note que o ângulo ADC é congruente ao ângulo BAP, pois CD e AP são paralelos e cortam a mesma reta, que possui os pontos B, A e D.
Podemos aplicar o teorema de Tales, que prova que os segmentos formados por uma reta transversal ao interceptar retas paralelas são congruentes. Assim, pelo teorema de Tales:
\(\frac{\overline{AB}}{\overline{BP}}=\frac{\overline{AD}}{\overline{PC}}\)
Note que o triângulo ACD é isósceles, pois a soma dos ângulos ACD +ADC é igual a 2x. Logo, cada um desses ângulos mede x.
Sendo o triângulo ACD isósceles, o segmento \(\overline{AC}\) possui a mesma medida que o segmento \(\overline{AD}\).
Dessa forma, temos:
\(\frac{\overline{AB}}{\overline{BP}}=\frac{\overline{AC}}{\overline{PC}}\)
Fica assim demonstrado o teorema da bissetriz interna.
Leia também: Teorema de Pitágoras — o teorema que pode ser aplicado em qualquer triângulo retângulo
Exercícios resolvidos sobre teorema da bissetriz interna
Questão 1
Calcule a medida do lado AB no triângulo a seguir, sabendo que AD é bissetriz do ângulo A.
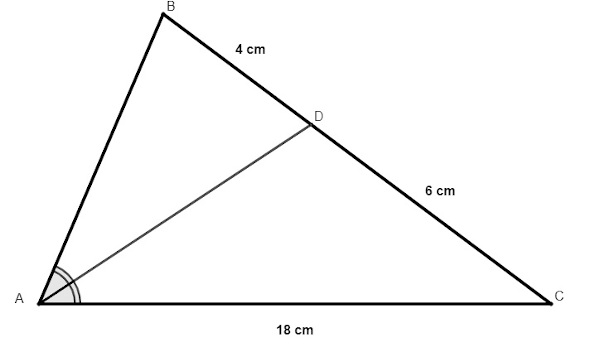
A) 10 cm
B) 12 cm
C) 14 cm
D) 16 cm
E) 20 cm
Resolução:
Alternativa B
Sendo x a medida do lado AB, pelo teorema da bissetriz interna temos que:
\(\frac{x}{4}=\frac{18}{6}\)
\(\frac{x}{4}=3\)
\(x=4\cdot3\)
\(x=12\ cm\)
Questão 2
Analise o triângulo a seguir e calcule o comprimento do segmento BC.
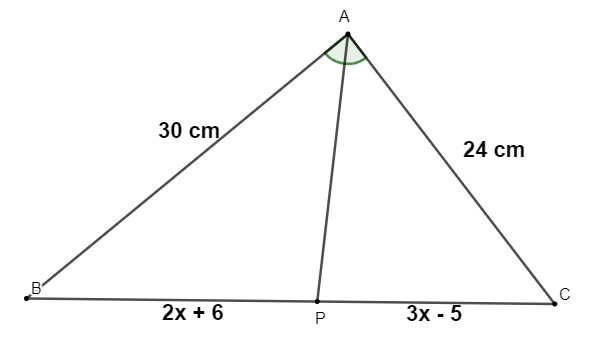
A) 36 cm
B) 30 cm
C) 28 cm
D) 25 cm
E) 24 cm
Resolução:
Alternativa A
Pelo teorema da bissetriz interna:
\(\frac{30}{2x+6}=\frac{24}{3x-5}\)
Multiplicando cruzado:
\(30\left(3x-5\right)=24\left(2x+6\right)\)
\(90x-150=48x+144\)
\(90x-48x=150+144\)
\(42x=294\)
\(x=\frac{294}{42}\)
\(x=7\ cm\)
Sabendo a medida de x, obtemos:
BC = 2x + 6 + 3x – 5
BC = \(2\cdot7+6+3\cdot7-5\)
BC = \(\ 36\ cm\)