A média harmônica é utilizada para representar, por um único valor, um conjunto de grandezas que possuem relação inversamente proporcional. Na estatística é bastante comum recorrer-se a uma média para representar um conjunto de dados, logo, há outras médias conhecidas e mais comuns, como a média aritmética, a média ponderada e a média geométrica. Cada uma delas possui aplicações específicas e é mais interessante de ser aplicada dependendo do tipo de grandeza com que estamos trabalhando.
Existem várias situações com grandezas inversamente proporcionais em que a média harmônica torna-se a média mais interessante para representar esse conjunto. É o caso, por exemplo, de problemas com escoamento de água, que trabalham com as grandezas tempo e vazão, quanto maior a vazão, menor o tempo, o que torna tais grandezas inversamente proporcionais.
Problemas que envolvem densidade e volume, ou tempo e velocidade, também costumam ser resolvidos com o auxílio da média harmônica. Dado um conjunto, a média harmônica é calculada como a quantidade de elementos no conjunto, dividida pela soma do inverso de cada elemento do conjunto.
Leia também: Medidas estatísticas: médias aritmética, ponderada e geométrica

Tópicos deste artigo
- 1 - Fórmula da média harmônica
- 2 - Como se calcula a média harmônica?
- 3 - Quando se usa a média harmônica?
- 4 - Aplicações da média harmônica
- 5 - Exercícios resolvidos
Fórmula da média harmônica
Para calcular a média harmônica de um conjunto de valores, utilizamos o inverso de cada um deles, lembrando que o inverso de um número é representado pela fração 1 sob ele, por exemplo o inverso de x é:
![]()
Caso x seja uma fração, basta realizar a inversão entre o seu numerador e o seu denominador. Quando ele é um número inteiro, isso também é feito, mas o inverso de um número inteiro é 1 sobre ele. Conhecendo-se o inverso de um número, a média harmônica do conjunto (x1, x2, x3, ..., xn-1, xn) que possui um total de n elementos é calculada pela fórmula:
![]()
Mh: média harmônica
n: quantidade de elementos do conjunto
Como se calcula a média harmônica?
Para realizar-se o calculo da média harmônica, é necessário ter-se o domínio das operações com frações, tendo-se em vista a soma de frações com denominadores diferentes. Dessa forma, o domínio de operações com fração é essencial para o aprendizado de média harmônica.
Exemplo:
Encontre a média harmônica do conjunto {2, 4, 5, 6}.
Como o conjunto tem quatro elementos, então n = 4.
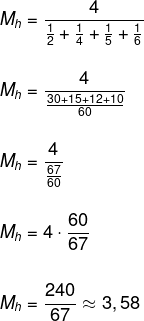
Veja mais: Definições básicas de estatística – conceitos fundamentais para o entendimento dessa área
Quando se usa a média harmônica?
Dado um conjunto de valores, é muito comum buscar-se um único valor que o representa para que decisões sejam tomadas. Na física, na química ou na própria matemática, buscar-se por uma medida central no conjunto tem muitas aplicações. Por isso existem várias medidas centrais, como a mediana, a média aritmética, a moda, a média geométrica, e, no caso a média harmônica, o que a torna necessária é o trabalho com grandezas inversamente proporcionais, bastante comum no nosso dia a dia, por exemplo, no cálculo da velocidade média, da densidade, da vazão da água, entre outras situações na matemática, na física e na química.
Aplicações da média harmônica
Dado qualquer conjunto de valores diferentes de zero, é possível encontrar-se a média harmônica entre eles, no entanto, existem situações que só se resolvem com ela.
Exemplo:
Cálculo da velocidade média
Dois amigos em viagem revesam-se para chegar a um determinado destino. Um deles dirigiu até exatamente a metade do percurso, e depois o outro assumiu o volante terminando o percurso. O primeiro deles manteve uma velocidade v1 = 80 km/h. Já o segundo, que estava com mais pressa, manteve uma velocidade de v2 = 120 km/h.
Aplicando na fórmula com n = 2:

Assim, a média de velocidade nesse percurso foi de 96 km/h.
Exemplo 2:
Cálculo da vazão de torneiras
Para encher uma piscina, uma das torneiras leva 15 horas, e a outra leva 10 horas. Existe uma terceira torneira que demora seis horas para encher a piscina. Caso as três torneiras fossem abertas ao mesmo tempo, quanto tempo elas levariam para encher toda a piscina?
1º passo: encontrar o tempo médio que uma torneira levaria para encher a piscina (n = 3):

Como as três serão ligadas simultaneamente no mesmo tanque, faremos a divisão 9 : 3 = 3.
Assim, elas levariam três horas.
Exemplo 3:
Cálculo da densidade
Considere-se a mistura de duas substâncias, A e B, em estado líquido de densidades 2 g/cm³ e 3 g/cm³. Caso fossem misturadas com a mesma massa de cada uma delas, sua densidade seria de:
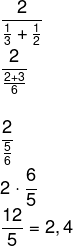
A densidade seria de 2,4 g/cm³.
Acesse também: Medidas de dispersão: amplitude e desvio
Exercícios resolvidos
Questão 1 - (Uel) Um automóvel subiu uma ladeira a uma velocidade média de 60 km/h e, em seguida, desceu a mesma ladeira a uma velocidade média de 100 km/h. A velocidade média desse veículo no percurso inteiro foi de:
A) 72 km/h
B) 75 km/h
C) 78 km/h
D) 80 km/h
E) 84 km/h
Resolução
Alternativa B
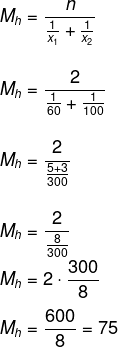
A velocidade média é de 75 km/h.
Questão 2 - (ESAF – ATA/MF – 2009) Existem duas torneiras para encher um tanque vazio. Se apenas a primeira torneira for aberta, ao máximo, o tanque encherá em 24 horas. Se apenas a segunda torneira for aberta, ao máximo, o tanque encherá em 48 horas. Se as duas torneiras forem abertas ao mesmo tempo, ao máximo, em quanto tempo o tanque encherá?
A) 12 horas
B) 16 horas
C) 20 horas
D) 24 horas
E) 30 horas
Resolução
Alternativa B
Primeiro vamos calcular o tempo médio que as torneiras levam para encher o tanque, como elas serão ligadas simultaneamente, faremos a divisão por dois a fim de encontrar o tempo necessário para que elas encham o tanque:

32 : 2 = 16 horas.