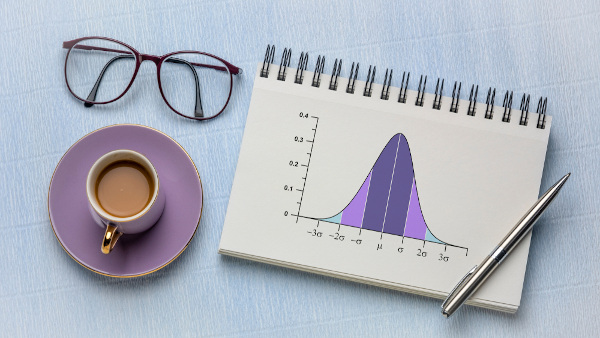
Estatística compreende o conjunto de técnicas empregadas para coleta e análise de dados, além da interpretação dos resultados e conclusões a respeito da população de estudo.
População corresponde ao conjunto de todos os indivíduos que partilham uma característica de interesse. Por exemplo, quando uma pesquisa eleitoral é realizada, o interesse é estudar a opinião dos eleitores de uma determinada região (município, estado, nação). Assim, a população de estudo é formada somente de eleitores; as pessoas residentes nesse local, mas que não são eleitores (as crianças, por exemplo), não fazem parte dessa população. Podemos considerar ainda o caso de um pesquisador marinho estudando a vida das baleias jubartes. Nesse caso, a população é formada apenas de baleias, e mais especificamente, baleias jubartes. Outras espécies de baleiras não pertencem a essa população. É importante enfatizar que o conceito de população está diretamente ligado ao objetivo do estudo.
Quando não é possível estudar toda uma população, recorre-se a apenas uma parte representativa dessa população. Essa parte é denominada amostra. Em ambos os exemplos anteriores, para se conduzir a pesquisa, seria necessário considerar uma amostra, já que não é possível perguntar a todos os eleitores sua opinião, nem acompanhar a vida de todas as baleias. Existem ocasiões em que é possível estudar toda a população de interesse e nesse caso a amostragem é dispensável. Por exemplo, se o professor de matemática tem o interesse de estudar o desempenho no vestibular dos alunos de uma turma em um colégio específico, não é necessário tomar uma amostra, já que o tamanho da população é pequeno e obter os dados de toda a população torna-se fácil.
De modo geral, em uma pesquisa não é coletado apenas uma ou outra característica de interesse. Normalmente se obtém vários dados de vários indivíduos. Cada característica específica é denominada variável e pode ser classificada segundo o tipo de informação que representa. Uma variável qualitativa ordinal separa os indivíduos em classes de qualidade que obedecem algum ordenamento. No caso dos estudos com baleias, o pesquisador pode separá-las em grupos segundo a idade, por exemplo, jovens, adultas, velhas. Existe uma relação de ordem entre esses grupos. No caso do estudo eleitoral, podemos separar os eleitores por regiões geográficas (norte, nordeste, sul, sudeste, centro-oeste), mas nesse caso não existe uma ordem entre os grupos. Essa variável é classificada como variável qualitativa nominal, pois separa os indivíduos em grupos segundo uma qualidade, mas não é possível estabelecer um ordenamento entre eles.
Além das variáveis que representam qualidade, existem as que representam quantidade, sugestivamente chamadas, variáveis quantitativas. Essas também são separadas em dois grupos: as quantitativas discretas e as quantitativas contínuas. Uma variável quantitativa discreta está associada aos dados de contagem, tais como quantidade de alunos aprovados, idade de cada eleitor, total de passageiros em um avião ou baleias que encalham durante uma estação. Esse tipo de variável sempre assume valores inteiros. Finalmente, uma variável pode ser classificada em variável quantitativa contínua, e, nesse caso, assume valores reais provenientes de um valor medido, assim como altura, peso, área de uma região ou valor a ser pago em um produto.