Entre as posições relativas de duas retas, podem ser encontradas as retas paralelas e coincidentes. Essas últimas são o que conhecemos como retas transversais. Quando um feixe de retas paralelas é cortado por uma transversal, podemos observar algumas propriedades importantes para a Matemática, entretanto, antes de discutir essas propriedades, é bom ter clareza em relação aos conceitos de retas paralelas e transversais.
Feixe de retas paralelas e reta transversal
Duas retas são chamadas paralelas quando pertencem a um mesmo plano e não possuem nenhum ponto em comum, isto é, elas não se encontram em lugar algum em toda a sua extensão – que é infinita.
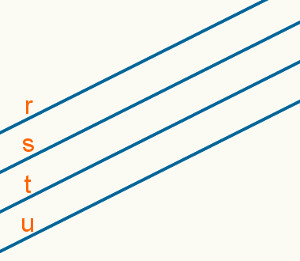
Um conjunto formado por duas ou mais retas paralelas no plano é o que conhecemos como feixe de retas paralelas. A seguir, observe uma imagem que contém um feixe com quatro retas paralelas. (Observação: não é possível desenhar uma reta completa porque ela é infinita. Assim, analisaremos uma representação possível das retas).
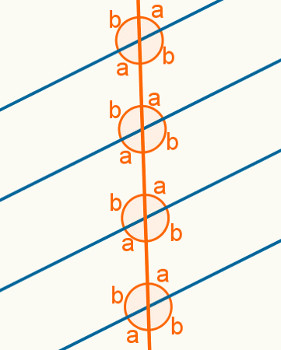
No feixe da imagem acima, qualquer reta que tenha um ponto em comum com a reta r terá também um ponto em comum com as retas s, t e u e será chamada de reta transversal. A imagem a seguir mostra um exemplo de uma reta transversal a esse feixe de retas paralelas.
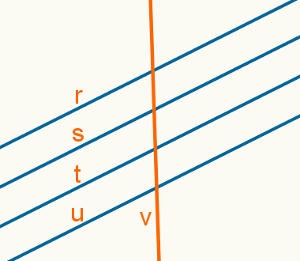
Propriedades
1 – Em um feixe de retas paralelas, ângulos correspondentes são congruentes. A saber, os ângulos correspondentes são aqueles que ocupam a mesma posição, mas em retas paralelas distintas. Sabendo que ângulos opostos pelo vértice também são congruentes, em um feixe de retas paralelas, os seguintes ângulos são congruentes:
2 – Se um feixe de retas paralelas divide uma reta transversal r em segmentos congruentes, então dividirá qualquer outra reta transversal s em segmentos também congruentes. A imagem a seguir mostra um exemplo do comprimento dos segmentos da reta s, quando todos os segmentos da reta r são congruentes.
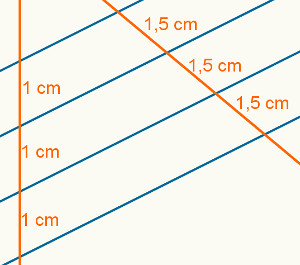
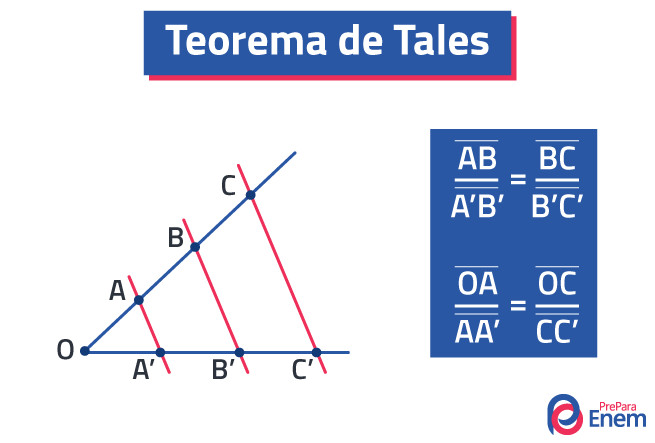
3 – Se um feixe de retas paralelas corta uma transversal em segmentos de retas proporcionais, então cortará qualquer outra transversal em segmentos de reta com a mesma proporção (Teorema de Tales). A imagem a seguir mostra como essa proporcionalidade é observada.
AB = BC = CD
EF FG GH
Aproveite para conferir nossas videoaulas sobre o assunto: