Área do cilindro

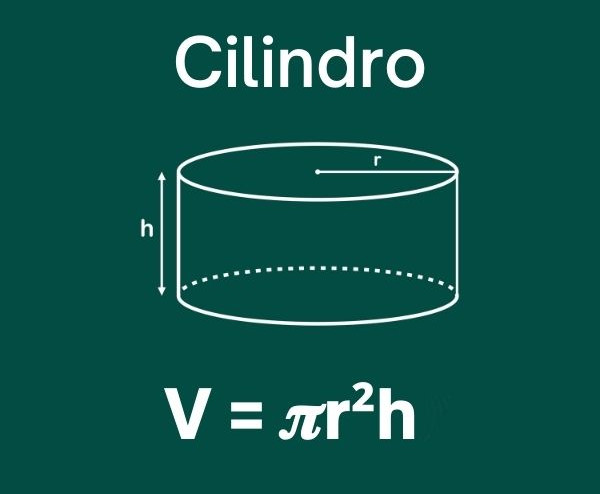
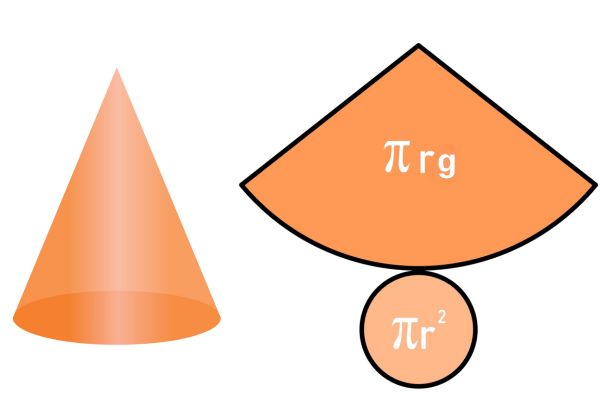
A área do cilindro é a medida da área superficial total desse sólido geométrico. Um cilindro é um corpo redondo composto por duas bases circulares congruentes e paralelas e pela reunião de todos os segmentos de reta cujas extremidades estão em cada um desses círculos.

Para poder calcular a área desse sólido é necessário conhecer a medida de sua altura e do raio de sua base. No caso do cilindro reto, é possível determinar por meio de uma fórmula a sua área total, que consiste na soma da sua área lateral (cuja planificação é um retângulo) com a área de suas duas bases (cujos formatos são círculos).

Leia também: Fórmulas do cálculo de área das principais figuras planas

Tópicos deste artigo

• 1 - Resumo sobre a área de um cilindro
• 2 - Videoaula sobre a área de um cilindro
• 3 - O que é cilindro?
• 4 - Como calcular a área do cilindro?
  • Área da base do cilindro
  • Área lateral do cilindro
  • Área total do cilindro
• 5 - Outros exemplos de cálculo da área do cilindro
• 6 - Exercícios resolvidos sobre área do cilindro

Resumo sobre a área de um cilindro

• O cilindro é um corpo redondo formado por duas bases circulares paralelas e segmentos de reta com extremidades nesses círculos.

• A área do cilindro (ou área total) é a soma da área de suas duas bases com sua área lateral.

• A área da base do cilindro de raio r é dada por: \(A_b=πr^2\).

• A área lateral do cilindro de raio r e altura h  é dada por: \(A_l=2πr⋅h\).

• A área do cilindro e raio r e altura h é dada por: \(A_t=2πr⋅(r+h)\).

Videoaula sobre a área de um cilindro

O que é cilindro?

O cilindro é um sólido geométrico pertencente à classe dos corpos redondos. É composto de duas bases circulares congruentes presentes em dois planos paralelos distintos e é formado pela reunião de todos os segmentos de reta cujas extremidades estão em cada um desses dois círculos, paralelos ao segmento que une os centros deles.

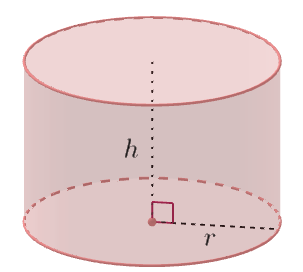
Entre seus principais elementos, podemos destacar o raio r  dos círculos que formam suas bases e a altura h, que indica a distância dos dois planos das bases.

Como calcular a área do cilindro?

A área de um cilindro (ou área total de um cilindro) é a soma da área lateral desse sólido e da área das duas bases circulares que o formam.

Quando o cilindro é reto, ou seja, no caso de o segmento que une os centros dos dois círculos ser perpendicular a eles, é possível estabelecer uma fórmula que determina o valor da área desse cilindro.

Para isso, pode-se observar a planificação desse sólido e como é calculada a área separada de cada figura plana que a compõe.

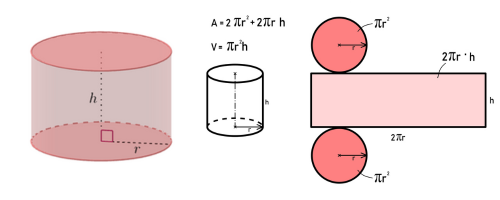
Veja a seguir como calcular cada uma das áreas superficiais do cilindro.

• Área da base do cilindro

As bases do cilindro são círculos congruentes, ou seja, dois círculos que possuem o mesmo raio. Assim, para calcular a área da base de um cilindro é preciso saber calcular a área de um círculo.

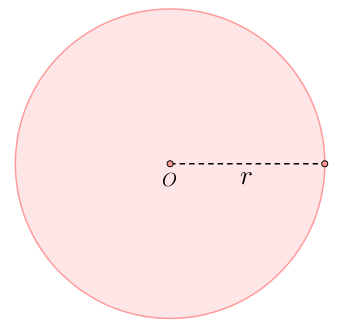
Sabendo a fórmula da área de um círculo, pode-se descrever a área da base do cilindro da seguinte forma:

Exemplo: Encontre a área da base de um cilindro cujo raio mede 3 cm.

Como visto, a área da base de um cilindro é relacionada à área de um círculo de raio r. Assim,

Área da base = Área do círculo

\(A_b =π⋅(3)^2=9π\ cm^2\)

• Área lateral do cilindro

A superfície lateral de um cilindro é formada pelas geratrizes dele, ou seja, pelos segmentos de reta cujas extremidades correspondentes encontram-se sobre as circunferências das bases.

No caso de um cilindro reto, a planificação desse sólido mostra que sua superfície lateral pode ser expressa por uma região retangular cujo comprimento é o mesmo comprimento das circunferências das bases e a largura é a altura do cilindro.

A partir da fórmula da área de um retângulo, pode-se representar a área lateral do cilindro reto da seguinte forma:

Exemplo: Calcule a área lateral de um cilindro cujo raio mede 3 cm e a altura mede 5 cm.

Utilizando a fórmula para a área lateral e substituindo os valores dados do raio e da altura, tem-se

Área lateral = \((2⋅π⋅r)⋅h\)

\(A_l =(2⋅π⋅3)⋅5=30π\ cm^2\)

• Área total do cilindro

A área total de um cilindro é a soma da área de suas duas bases com sua área lateral.

Exemplo: Determine a área total de um cilindro cujo raio mede 3 cm e a altura mede 5 cm.

A área da base e a área lateral de um cilindro com essas medidas já foi calculada anteriormente. Assim, a área total desse cilindro é dada por:

Área total do cilindro = 2 ⋅  Área da base + Área lateral

\(A_t =2⋅ 9π\ cm^2+30π\ cm^2\)

\(A_t =48π\ cm^2\)

Outros exemplos de cálculo da área do cilindro

Nos tópicos anteriores foi explorada a fórmula das áreas de um cilindro de forma individual e percebeu-se que para calcular a área total é necessário ter as medidas da altura do cilindro reto e o raio do círculo da base.

Assim, para calcular a área de um cilindro (ou área total), utiliza-se a fórmula:

Área do cilindro = \(2⋅π⋅r^2+2⋅π⋅r⋅h\)

ou ainda

Área do cilindro = \(2⋅π⋅r⋅(r+h)\)

Exemplo 1: Qual a área de um cilindro cuja altura mede 3,5 metros e o raio do círculo da base mede 1,5 metros?

Utilizando a fórmula da área do cilindro e substituindo os dados fornecidos da altura e do raio, tem-se que

Área do cilindro = \(2⋅π⋅r⋅(r+h)\)

\(A = 2⋅π⋅1,5⋅(1,5+3,5)\)

\(A = 3π⋅(5)=15π\ m^2\)

Exemplo 2: Qual a altura de um cilindro cuja área total mede 48π cm² e o raio do círculo da base mede 4 cm?

Neste exemplo, dada a área total e o raio da base, é necessário descobrir o valor da altura do cilindro. Utilizando a fórmula da área do cilindro:

Área do cilindro = \(2⋅π⋅r⋅(r+h)\)

\(48π=2⋅π⋅4⋅(4+h)\)

\(\frac{48π}{8π}=4+h\)

\(h=6-4=2\ cm\)

Portanto, a altura desse cilindro é de 2 cm.

Leia também: Como se calcula a área de um prisma?

Exercícios resolvidos sobre área do cilindro

Questão 1

(Enem 2014) Uma empresa que organiza eventos de formatura confecciona canudos de diplomas a partir de folhas de papel quadradas. Para que todos os canudos fiquem idênticos, cada folha é enrolada em torno de um cilindro de madeira de diâmetro d em centímetros, sem folga, dando-se 5 voltas completas em torno de tal cilindro. Ao final, amarra-se um cordão no meio do diploma, bem ajustado, para que não ocorra o desenrolamento, como ilustrado na figura.

Em seguida, retira-se o cilindro de madeira do meio do papel enrolado, finalizando a confecção do diploma. Considere que a espessura da folha de papel original seja desprezível.

Qual é a medida, em centímetros, do lado da folha de papel usado na confecção do diploma?

a) πd

b) 2πd

c) 4πd

d) 5πd

e) 10πd

Resolução

A questão exige que saibamos qual é o comprimento da folha de papel que será enrolada por completo no cilindro 5 vezes. Sabemos que o comprimento da circunferência é de \(2⋅π⋅r\), e, portanto, multiplicando esse valor por 5 determina-se o comprimento da folha de papel:

\(5⋅(2⋅π⋅r) = 10πr\)

Além disso, sabe-se que o raio r de uma circunferência é exatamente a metade da medida do seu diâmetro d, ou seja, \(r=\frac{d}2\). Logo,

Comprimento da folha = \(10πr=10π⋅(\frac{d}2)=5πd\)

A alternativa correta é a alternativa d.

Questão 2

(CEV-Urca 2021) Em um cilindro circular reto de altura 1 m, sabe-se que a razão entre a área lateral e a área total é 13. Qual o valor do raio da base?

a) 1 m

b) 2 m

c) 3 m

d) 4 m

e) 5 m

Resolução

Para resolver esta questão, deve-se calcular a razão entre a área lateral e a área total de um cilindro e igualar o resultado a um terço:

\(\frac{Área\ lateral}{Área\ total}=\frac{1}3\)

\(\frac{2πr⋅h}{2πr⋅(r+h)}=\frac{1}3\)

\(\frac{h}{r+h}=\frac{1}3\)

\(3h=r+h\)

\(r=2h\)

Assim, como o problema fornece o dado de que a altura mede 1 m, então o raio do cilindro mede \(2⋅1=2\ m\).

A alternativa correta é a alternativa b.

Fontes

ALMEIDA, Célio Pinto de. Geometria espacial. 1. ed. Rio de Janeiro: G. Ermakoff, 2018.

DOLCE, Osvaldo; NICOLAU, José. Fundamentos de matemática elementar 10 – Geometria espacial. 5. ed. Santos: Atual, 1993.