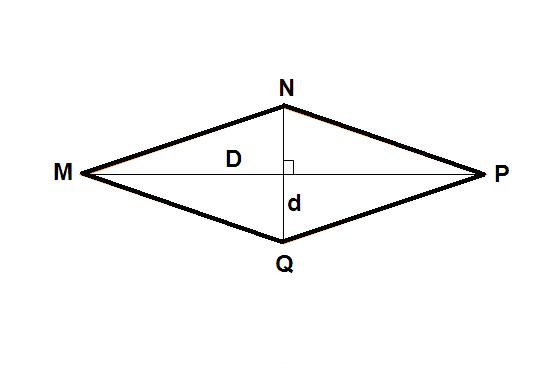
O losango é um quadrilátero que possui lados opostos paralelos e congruentes e duas diagonais que se cruzam exatamente no ponto médio de cada uma e são perpendiculares. Todo losango é também paralelogramo. Chamaremos de D a diagonal maior e d a diagonal menor.
Considere um losango de diagonais D e d.
A sua área será dada por:

Onde,
D → é a diagonal maior
d → é a diagonal menor
Observe que a área do losango é a metade do produto das medidas de suas diagonais.
Exemplo 1. Calcule a área de um losango de diagonais medindo 7 cm e 4 cm.
Solução: foram dados D = 7 cm e d = 4 cm. Dessa forma, basta substituir os valores na fórmula da área. Assim,
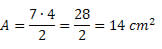
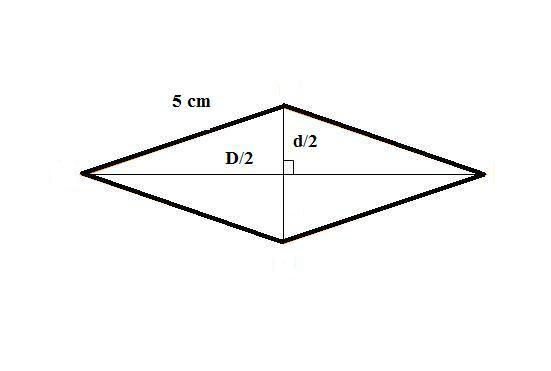
Exemplo 2. Calcule a área de um losango de 5 cm de lado e diagonal menor medindo 6 cm.
Solução: para o cálculo da área precisamos conhecer as medidas das duas diagonais, mas o problema nos forneceu apenas a da diagonal menor. Dessa forma, precisamos determinar a medida da diagonal maior.
Utilizando o teorema de Pitágoras, temos que:
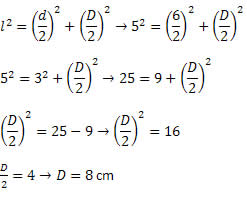
Conhecendo as medidas das duas diagonais, basta utilizar a fórmula da área. Assim,
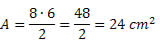
Exemplo 3. Considere um losango com área de 27 cm2 e diagonal maior medindo 9 cm. Qual a medida do lado desse losango?
Solução: para determinarmos a medida do lado do losango é preciso conhecer as medidas das duas diagonais. Assim, temos que encontrar a medida da diagonal menor. Como sabemos o valor da área do losango e a medida da diagonal maior, segue que:
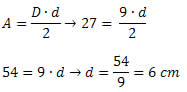
Conhecendo as medidas das duas diagonais, aplicamos o teorema de Pitágoras:
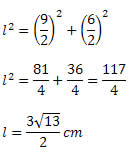



.JPG)