Plano inclinado

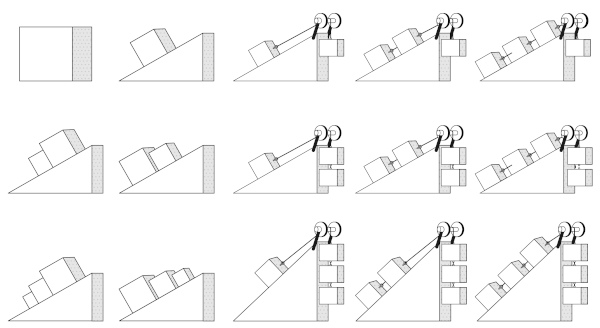
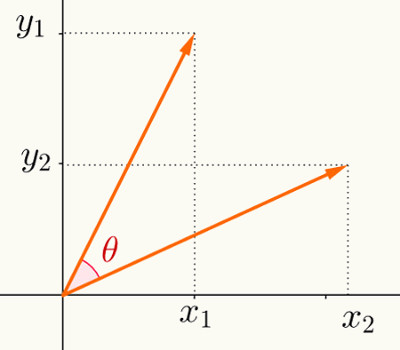O plano inclinado é a representação de um plano que possui certo ângulo em relação à superfície horizontal. Em decorrência disso, a direção das forças que atuam nesse corpo é alterada e, assim, é necessário trabalhar com notação vetorial para descobrir os valores dessas forças.

 Se o plano não possui atrito, as únicas equações abordadas são as das forças normal e peso, que são idênticas: N = P = m . g . cosθ. Se o plano possuir uma força de atrito contrária ao movimento do objeto, além das equações anteriores, é necessário utilizar a força de atrito, F_at = µ . N.

Leia também: Quais são os conceitos básicos de movimento?

Tópicos deste artigo

• 1 - Resumo sobre plano inclinado
• 2 - Videoaula sobre plano inclinado
• 3 - O que é plano inclinado?
  • Exemplos de plano inclinado
• 4 - Quais são os tipos de planos inclinados?
  • Plano inclinado sem atrito
  • Plano inclinado com atrito
• 5 - Quais são as fórmulas do plano inclinado?
• 6 - Aceleração no plano inclinado
• 7 - Exercícios resolvidos sobre plano inclinado

Resumo sobre plano inclinado

• Plano inclinado é uma superfície que possui um ângulo em relação à horizontal.

• Para trabalhar com as forças que atuam nos corpos em planos inclinados, é necessário usar notação vetorial.

• A força normal é perpendicular ao plano inclinado (forma um ângulo de 90°).

• A força peso é perpendicular ao solo.

• A força peso é dividida nas componentes x e y por meio da decomposição vetorial.

• A componente Y se anula com a força normal.

• A componente X se torna a força resultante do objeto.

• A aceleração de objetos em planos sem atrito é constante e está relacionada com a aceleração gravitacional e o seno do ângulo de inclinação: a = g . senθ.

Videoaula sobre plano inclinado

O que é plano inclinado?

O plano inclinado é um plano que possui uma diferença de ângulo em relação à superfície horizontal. Dessa forma, possui uma altura e, com isso, altera a direção das forças que atuam sobre o plano e os corpos que estejam sobre ele.

• Exemplos de plano inclinado

Alguns planos inclinados com os quais nos deparamos no dia a dia são:

• ruas inclinadas

• rampas para a passagem de cadeirantes

• escadas rolantes

Qualquer superfície que não esteja paralela ao solo pode ser considerada um plano inclinado.

Veja também: Trabalho da força normal sobre um corpo

Quais são os tipos de planos inclinados?

• Plano inclinado sem atrito

Quando consideramos um sistema ideal, sem a aplicação de forças de resistência, como a resistência do ar e o atrito, consideramos esse sistema um plano inclinado sem atrito. Nesses casos, apenas consideramos as forças do próprio objeto no plano inclinado.

• Forças do plano inclinado sem atrito

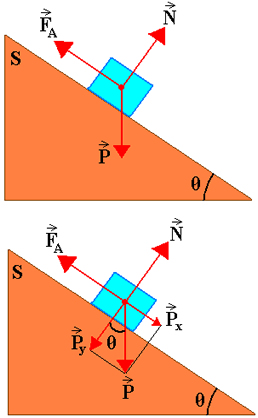
Sem considerar o atrito, as únicas forças que atuam no corpo são:

• força peso

• força normal

• força que movimenta o objeto

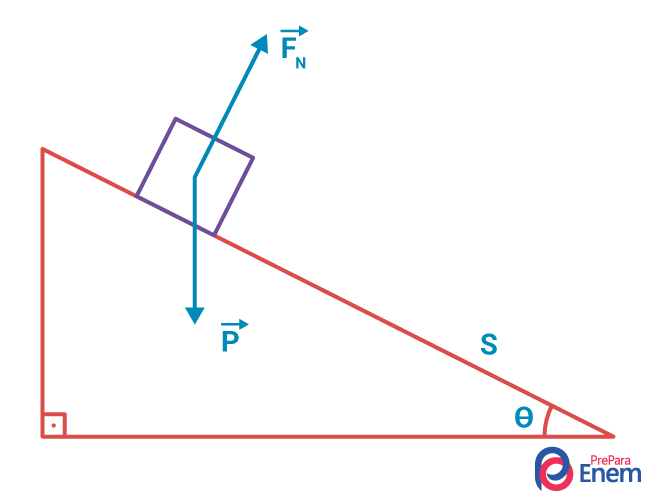
Essas forças representam a força resultante do sistema no plano inclinado. Elas possuem ângulos diferentes em relação ao solo, por isso a notação vetorial é necessária.

• Plano inclinado com atrito

Ao considerar o atrito do solo, é necessário representar uma força contrária no sistema, uma força que atrapalha o movimento dependendo do tipo de superfície em que o objeto esteja.

• Forças do plano inclinado com atrito

As três forças que aparecem no plano inclinado sem atrito também aparecem aqui, porém acrescentamos a força de atrito contrária ao movimento.

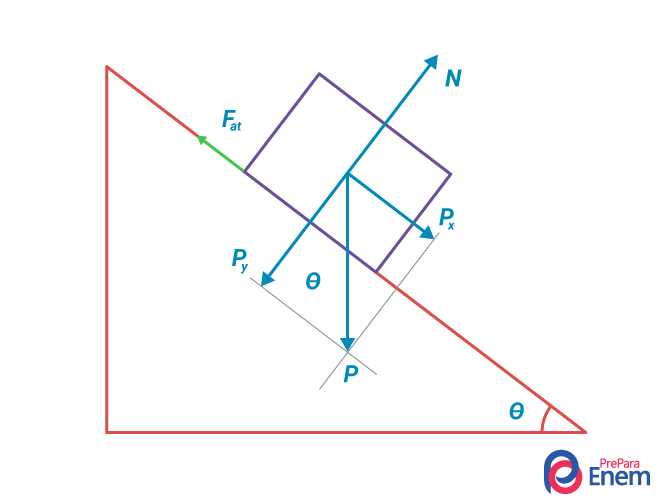
Essa força de resistência depende do material do objeto deslizando pela superfície e do material do qual a superfície é constituída. Quanto mais imperfeições e ranhuras, maior será a resistência do objeto com a superfície e mais difícil será deslizá-lo.

Quais são as fórmulas do plano inclinado?

Para o plano inclinado sem atrito, consideramos apenas a força normal, que é dada por:

N = m . g . cosθ

N → força normal (N)

m → massa do corpo (Kg)

g → aceleração da gravidade (m/s²)

cos θ → cosseno do ângulo de inclinação do plano

E a força peso, que é dada pela mesma equação:

P = m . g . cosθ

P → força normal (N)

m → massa do corpo (Kg)

g → aceleração da gravidade (m/s²)

cos θ → cosseno do ângulo de inclinação do plano

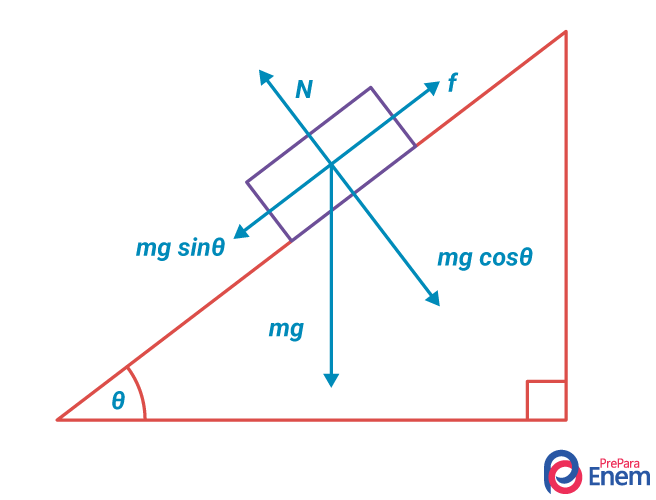
Realizando a decomposição dos vetores, é possível encontrar as componentes que formam a resultante do peso:

Assim, temos que:

Na componente do eixo x:

P_x = P . senθ

Na componente do eixo y:

P_y = P . cosθ

Pela decomposição, é possível observar que a normal e o peso na componente x são opostos, assim:

P_y = N

Então:

N = P . cosθ

Agora, para o plano inclinado com atrito, além dessas duas equações, é necessário encontrar o valor da força de atrito:

F_at = μ . N

N → força normal (N)

µ → coeficiente de atrito (adimensional)

Fat → força de atrito (N)

Aceleração no plano inclinado

Como o plano inclinado possui um ângulo em relação à superfície, haverá aceleração sobre os objetos que estiverem no plano, e essa aceleração será constante.

Pelo princípio fundamental da dinâmica, conhecido como 2ª lei de Newton, sabemos que força resultante é:

F = m . a

Como a componente x do peso não é anulada pela normal, ela se torna a força resultante do sistema. Então:

P_x = m . a

E:

P_x = P . senθ = m . a

Como peso é massa vezes aceleração da gravidade:

m . g . senθ = m . a

Agora, isolando a aceleração, em um plano inclinado sem atrito, temos:

a = g . senθ

Leia também: Segunda lei de Newton: como esse tema é cobrado no Enem?

Exercícios resolvidos sobre plano inclinado

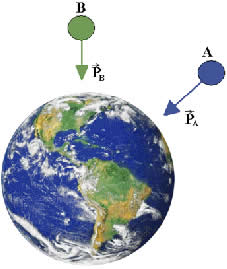
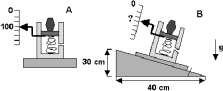
Questão 1 - (Fuvest) O mostrador de uma balança, quando um objeto é colocado sobre ela, indica 100 N, como esquematizado em A. Se tal balança estiver desnivelada, como se observa em B, seu mostrador deverá indicar, para esse mesmo objeto, o valor de:

A) 125 N

B) 120 N

C) 100 N

D) 80 N

E) 75 N

Resolução

Alternativa D

Encontrando a hipotenusa do plano inclinado, temos:

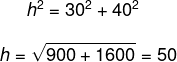
Com isso, descobrimos o cosseno do ângulo de inclinação do plano:

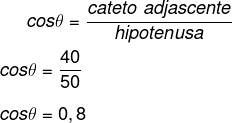
Agora, é possível encontrar a componente Y:

P_y = P . cosθ

P_y = 100 · 0,8

P_y = 80N

Questão 2 - (PUC-Rio) Um bloco de massa m é colocado sobre um plano inclinado cujo coeficiente de atrito estático = 1, como mostra a figura. Qual é o maior valor possível para o ângulo α de inclinação do plano de modo que o bloco permaneça em repouso?

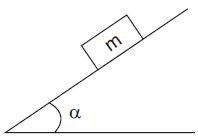
A) 30°

B) 45°

C) 60°

D) 75°

E) 90°

Resolução

Alternativa B

Para descobrir o ângulo do plano, é necessário encontrar o coeficiente de atrito:

P_x = F_at

P · senθ = N · µ

Como a normal pode ser encontrada por meio da componente Y do peso:

N = P_y = P · cosθ

Assim:

P · senθ = P · cosθ · µ

Isolando o coeficiente de atrito, achamos a equação da tangente do ângulo de inclinação:

Como o coeficiente de atrito vale 1, precisamos achar o ângulo que tem como tangente o valor 1, e, com a tabela trigonométrica, temos que esse ângulo é 45°.

Crédito da imagem

[1] Oliver Foerstner / Shutterstock