A aceleração centrípeta é uma grandeza física vetorial do movimento circular uniforme (MCU) com orientação radial para o centro da trajetória, sendo capaz de alterar a direção e o sentido da velocidade tangencial do corpo que descreve um movimento circular. Ela é calculada principalmente através da divisão entre o quadrado da velocidade escalar e o raio.
Resumo sobre aceleração centrípeta
- A aceleração centrípeta é uma aceleração que aparece durante os movimentos circulares, com orientação perpendicular para o centro da trajetória.
- A unidade de medida da aceleração centrípeta é m2/s .
- Ela é calculada principalmente através da divisão entre o quadrado da velocidade escalar e o raio.
- A aceleração centrípeta é calculada também através do produto entre o quadrado da velocidade angular e o raio.
- A aceleração centrípeta gerada pela rotação da Terra é de 0,03 m/s2 na Linha do Equador e nula nos polos.
- A força centrípeta é calculada através do produto entre a massa e a aceleração centrípeta de um corpo.
- Durante os movimentos circulares, a razão pela qual os corpos tendem a sair da trajetória é a inércia, e não a aceleração centrífuga, que é uma aceleração que não existe.
Videoaula sobre aceleração centrípeta
O que é a aceleração centrípeta?
A aceleração centrípeta é uma grandeza física estudada no movimento circular uniforme (MCU) presente em todos os corpos que realizam um movimento rotacional, sendo responsável pela variação da direção e do sentido da velocidade tangencial do corpo (velocidade com direção tangente à trajetória), como podemos ver na imagem abaixo.
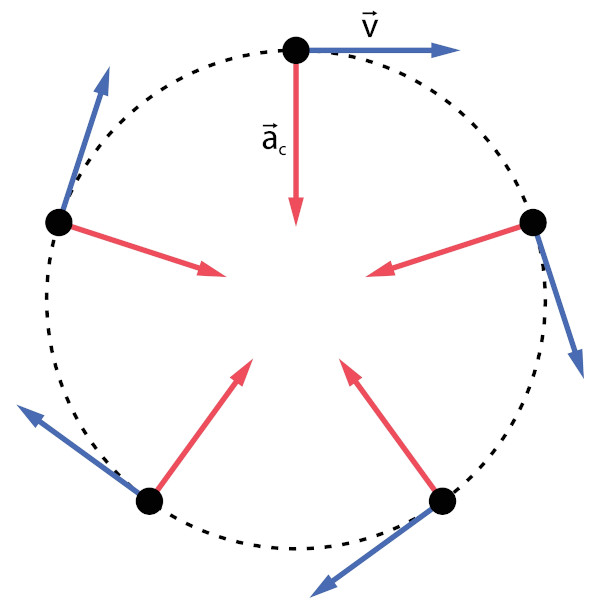
À medida que o raio da curva aumenta, a aceleração centrípeta do corpo diminui, e à medida que a velocidade do corpo aumenta, a aceleração centrípeta do corpo aumenta ao quadrado. Isso acontece porque a aceleração centrípeta é inversamente proporcional ao raio da curva e diretamente proporcional ao quadrado da velocidade do corpo em movimento.
Além disso, a aceleração centrípeta também é uma grandeza vetorial, então a sua orientação e módulo são:
- Módulo: calculado através das suas fórmulas.
- Direção: radial ou perpendicular, aquela que forma um ângulo de 90°.
- Sentido: apontando para o centro da trajetória.
De acordo com o Sistema Internacional de Unidades (SI), a unidade de medida da aceleração centrípeta é metros quadrados sobre segundos, representado por m2/s . Já pelo centímetro-grama-segundo (CGS), a unidade de medida da aceleração centrípeta é centímetros quadrados sobre segundos, representado por cm2/s .
Quais são as fórmulas da aceleração centrípeta?
→ Aceleração centrípeta relacionada à velocidade escalar e ao raio
\(a_{CP}=\frac{v^2}{R}\)
- aCP → aceleração centrípeta, medida em [m/s2] .
- v → velocidade escalar, medida em ms .
- R → raio da curva, medido em metros [m].
→ Aceleração centrípeta relacionada à velocidade angular e ao raio
\(a_{CP}=\omega^2\cdot R\)
- aCP → aceleração centrípeta, medida em [m/s2] .
- R → raio da curva, medido em metros [m ].
- ω → velocidade angular, medida em [rad/s].
Como calcular a aceleração centrípeta?
A aceleração centrípeta pode ser calculada a partir da fórmula que a relaciona à velocidade escalar e ao raio e a partir da fórmula que a relaciona à velocidade angular e ao raio. Abaixo, temos exemplos de como calculamos a aceleração centrípeta através de cada uma dessas fórmulas.
- Exemplo 1:
Qual a aceleração centrípeta de um corredor que treina ao redor de uma pista de raio de 100 m com uma velocidade de 25m/s?
Resolução:
Calcularemos a aceleração centrípeta através da fórmula que a relaciona à velocidade escalar e ao raio:
\(a_{CP}=\omega^2\cdot R\)
\(a_{CP}=2^2\cdot40\)
\(a_{CP}=4\cdot40\)
\(a_{CP}=160\ m/s^2\ \)
A aceleração centrípeta do corredor é de 6,25 m/s2 .
- Exemplo 2:
Qual a aceleração centrípeta de um ciclista que se desloca em uma trajetória circular de raio 40 m com velocidade angular igual a 2 rad/s?
Resolução:
Calcularemos a aceleração centrípeta através da fórmula que a relaciona à velocidade angular e ao raio:
\(a_{CP}=\omega^2\cdot R\)
\(a_{CP}=2^2\cdot40\)
\(a_{CP}=4\cdot40\)
\(a_{CP}=160\ m/s^2\ \)
A aceleração centrípeta do ciclista é de 160 m/s2.
Qual é a aceleração centrípeta da Terra?
A aceleração centrípeta ocasionada pela rotação da Terra é de 0,03 m/s2 na Linha do Equador e nula nos polos. Ela é anulada pela aceleração da gravidade, cujo valor é de aproximadamente 9,8 m/s2 , o que faz com que nós não a experienciemos.
Diferenças entre aceleração centrípeta e força centrípeta
A aceleração centrípeta e a força centrípeta são grandezas físicas intimamente relacionadas, mas completamente diferentes. Enquanto a aceleração centrípeta é uma aceleração capaz de alterar a direção e sentido do vetor velocidade, a força centrípeta é uma força capaz de alterar a direção da velocidade do corpo e o manter na trajetória circular, sendo calculada através da fórmula:
\(F_{CP}=m\cdot a_{CP}\)
- FCP → força centrípeta, medida em Newton [N] .
- m → massa do corpo, medida em quilograma kg.
- aCP → aceleração centrípeta, medida em [m/s2] .
O que é aceleração centrífuga?
A aceleração centrífuga é uma aceleração que não existe, sendo confundida com a inércia dos corpos em movimentos circulares, que é a tendência que os corpos têm de se manterem em movimento retilíneo com velocidade constante ou de se manterem em repouso quando o somatório das forças atuantes sobre ele é nulo.
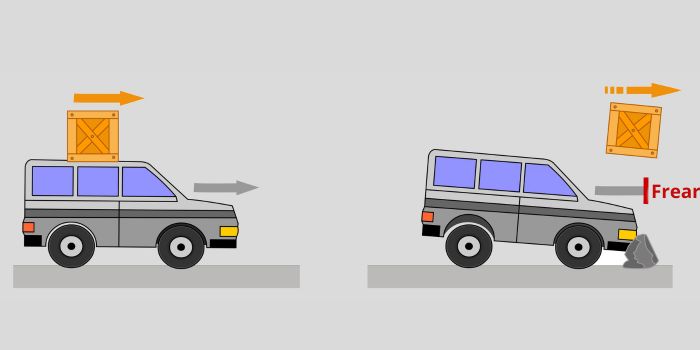
Saiba mais: Primeira lei de Newton — a lei que descreve o princípio da inércia
Exercícios resolvidos sobre aceleração centrípeta
Questão 1
(UEMG) Em uma viagem a Júpiter, deseja-se construir uma nave espacial com uma seção rotacional para simular, por efeitos centrífugos, a gravidade. A seção terá um raio de 90 metros. Quantas rotações por minuto (RPM) deverá ter essa seção para simular a gravidade terrestre? (considere g = 10 m/s²).
A) \(\frac{10}{\pi}\)
B) \(\frac{2}{\pi}\)
C) \(\frac{20}{\pi}\)
D) \(\frac{15}{\pi}\)
Resolução:
Alternativa A.
Para determinarmos quantas rotações por minuto deverá ter essa seção, calcularemos a frequência através da fórmula que relaciona a aceleração centrípeta à velocidade angular e ao raio:
\(a_{CP}=\omega^2\cdot R\)
Sabemos que a velocidade angular é 2∙π∙f , então:
\(a_{CP}=\left(2\cdot\pi\cdot f\right)^2\cdot R\)
\(10=4\cdot\pi^2\cdot f^2\cdot90\)
\(10=360\cdot\pi^2\cdot f^2\)
\(f^2=\frac{10}{360cdot\pi^2}\)
\(f^2=\frac{1}{36\cdot\pi^2}\)
\(f=\sqrt{\frac{1}{36\cdot\pi^2}}\)
\(f=\frac{1}{6\cdot\pi}\ rps\)
A frequência está em rotações por segundo, mas o enunciado pede em rotações por minutos, então vamos converter através de uma regra de três simples:
\(1s\ -\ \frac{1}{6\cdot\pi}\)
\(60\ s\ \ -\ x\)
\(x=\frac{1}{6\cdot\pi}\cdot60\)
\(x=\frac{60}{6\cdot\pi}\)
\(x=\frac{10}{\pi}\)
Questão 2
Um móvel executa movimento circular uniforme em uma trajetória de raio 40 cm com frequência de 1 Hz. A partir dessas informações, determine a aceleração centrípeta desse móvel.
Dados: π = 3.
A) 0,9 m/s2
B) 1,8 m/s2
C) 3,6 m/s2
D) 7,2 m/s2
E) 14,4 m/s2
Resolução:
Alternativa E.
Primeiramente, converteremos o raio de centímetros para metros:
\(40\ cm\ =\ 0,4\ m\)
Depois, calcularemos a velocidade angular através da fórmula que a relaciona à frequência:
\(\omega=2\cdot\pi\cdot f\)
\(\omega=2\cdot3\cdot1\)
\(\omega=6\ rad/s\)
Por fim, calcularemos a aceleração centrípeta através da fórmula que a relaciona à velocidade angular e ao raio:
\(a_{CP}=\omega^2\cdot R\)
\(a_{CP}=6^2\cdot0,4\)
\(a_{CP}=36\cdot0,4\)
\(a_{CP}=14,4\ m/s^2\)
